Оптимизация электрических распределительных сетей, страница 5

2.  Влияние технико-экономической соразмерности исследуемого объекта или, иначе, определение относительных затрат (долей), приходящихся на каждое слагаемое уравнения (1.14) в экономическом варианте. Такая задача возникает при распределении заданных суммарных затрат между отдельными элементами, входящими в электроэнергетическую систему.

3.  Исследование экономической устойчивости модели. Эта задача состоит в определении степени изменения затрат при отклонении оптимизируемого параметра от его экономического значения. Считают, что если достаточно большие изменения параметра приводят к незначительному изменению затрат, то такая модель экономически устойчива к изменению данного параметра. В качестве нормированного увеличения затрат по сравнению с экономическим значением, в пределах которого модель можно считать экономически устойчивой к изменению оптимизируемого параметра, обычно принимают 5%. Тогда варианты модели, отличающейся от экономического варианта по затратам на 5% образуют зону равноэкономичности (см рис. 1).

4.  Исследование чувствительности экономического значения параметра и затрат к изменению исходных данных, входящих в обобщенные константы Аi. Рассматриваемая задача вызвана необходимостью оценки влияния погрешности исходных данных на значение экономически целесообразного значения оптимизируемого параметра и экономических затрат. Если же заданы погрешности значений этих параметров, то формулы чувствительности позволяют определить допустимые погрешности исходных данных.

5.  Определение оптимального варианта, т.е. экономически целесообразных значений параметров и затрат, удовлетворяющих минимуму приведенных затрат с учетом технических ограничений, которые накладываются на изменение оптимизируемого параметра. Технические ограничения целесообразно разделить на два класса: дискретные и функциональные. К первому классу относятся ограничения, удовлетворяющие неравенству:

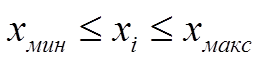 (1.15),

а также ограничения, обусловленные дискретностью шкал параметров.

К функциональным ограничениям относятся те, которые накладываются на изменение параметров аналитическими зависимостями вида:

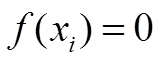 (1.16)

в которые параметры входят в качестве независимых переменных.

1.3 Решение пяти задач критериального анализа при оптимизации числа внутрицеховых ТП.

Сформулированные выше основные технико-экономические задачи критериального анализа решим методом, разработанным в МЭИ по руководством проф. В. А. Веникова. Преимущества этого метода по сравнению с другими существующими оптимизационными методами заключается в том, что он придает исследованию обобщенный характер, рационально использует информацию о исходных данных и результатах ранее сделанных расчетов и позволяет решать ряд задач, не зная численного значения исходных данных.

Критериальный метод анализа базируется на последовательном использовании теории подобия для решения оптимизационных технико-экономических задач. Рассмотрим применение данного метода для исследования модели (1.14), в начале для переменной части (исключаем А0). Определим предварительно методом интегральных аналогов выражение для экономических значений критериев подобия, разделив почленно уравнение

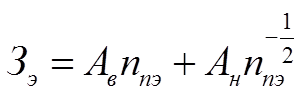 (1.17)

на приведенные затраты Зэ:

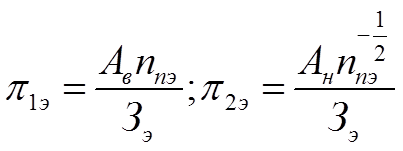 (1.18)

В общем случаи изменение констант Аi и параметра nп приводят к изменению численных значений критериев подобия, но их сумма всегда:

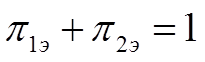 (1.19)

Уравнения (1.18) при известных исходных данных Аi позволяет определить экономические значения параметров и затрат, если предположить, что известны также критерии подобия. Запишем уравнения (1.18) в ином виде:

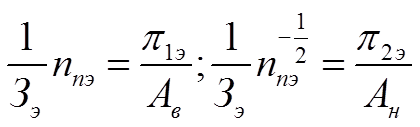 (1.20)

и прологарифмировав их, получим систему линейных уравнений относительно неизвестных ln xjэ и ln Зэ:

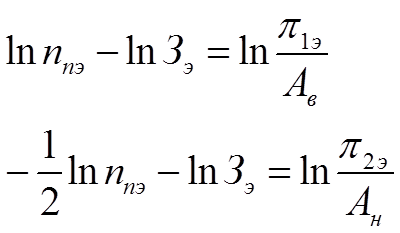   (1.21),

или в матричной форме:

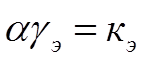  (1.22),

где a - матрица показателей степени оптимизируемого параметра;

gэ – матрица вектор экономических показателей;

кэ – матрица исходных данных.

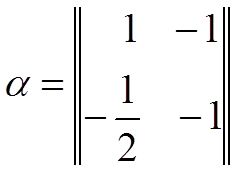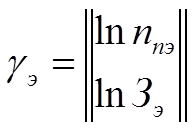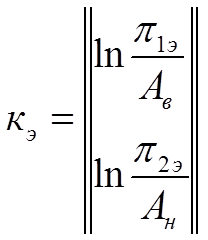;      ;            (1.23)

Исходная модель (1.14) удовлетворяет условию каноничности, когда число слагаемых в уравнении на единицу больше, чем число оптимизируемых параметров (у нас слагаемых – два, а оптимизируемый параметр один), а матрица a неособенная (ее определитель отличен от нуля).

Из уравнения (1.22) можно определить вектор уэ:

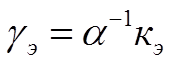  (1.24)