Оптимизация электрических распределительных сетей, страница 6

Пропотенцировав уравнение (1.24) находим выражение экономических значений параметра и затрат, предварительно находим обратную матрицу:

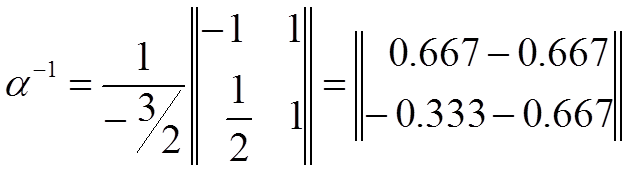  (1.25)

Согласно [1]:

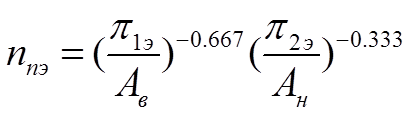 (1.26.1)

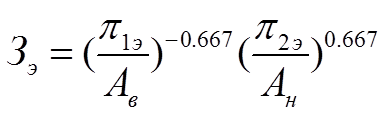 (1.27),

Кроме того, в [2], исходя из первой и положительной второй производной модели (1.6) с учетом (1.7) – (1.9), приводится формула для определения экономического числа внутрицеховых ТП:

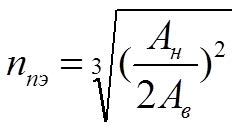 (1.26.2)

В выражениях (1.26.1) и (1.27) значения степеней множимых являются членами обратной матрицы (1.25). Определим экономические значения критериев подобия, используя уравнение:

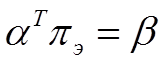  (1.28),

где

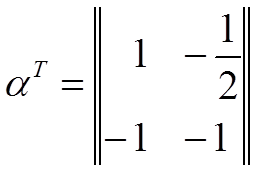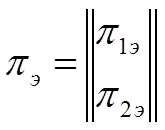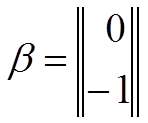;      ;            (1.29),

тогда получаем:

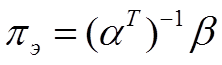  (1.30),

где

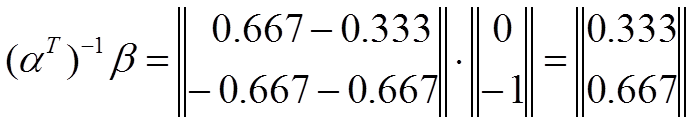  (1.31.1)

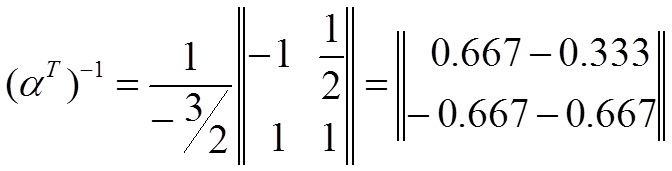  (1.31.2)

Т.о. получаем, исходя из (1.30) и (1.31), что:

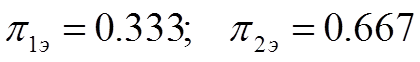 (1.32)

Получили, что критерии подобия не зависят от констант, а определяются только показателями степени оптимизируемого параметра. Т.е. получили, что для канонических моделей экономические значения критериев подобия могут быть найдены непосредственно из обратной матрицы a и они соответствуют экономическому значению затрат, взятых с обратным знаком. Они показывают долю суммарных затрат, приходящихся на отдельное слагаемое исходной модели для экономического варианта, т.е. позволяют решить вторую задачу технико-экономического анализа. В нашем случаи получаем, что не зная всех исходных данных для модели (1.17) можно сказать, что затраты на стороне ВН составят 33% и на НН – 66% от общих суммарных затрат.

Чтобы решить первую задачу, потребуются исходные данные и тогда по формулам (1.26.1) и (1.27) определим численные значения экономических значений оптимизируемого параметра и затрат.

Для решения третьей задачи запишем исходное уравнение (1.14) в критериальной форме. За базисные значения принимаем экономический вариант.

Выражая значения оптимизируемого параметра и затрат произвольных вариантов в относительных единицах

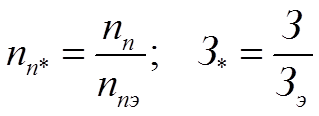 (1.33)

запишем исходную модель в виде:

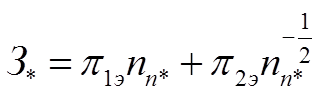 (1.34),

или с учетом (1.32):

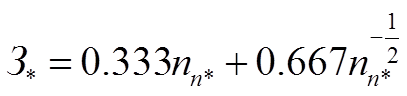 (1.35)

Уравнение (1.34) называется критериальным уравнением исходной модели или критериальной моделью исследуемого объекта. Оно носит обобщенный характер и в явном виде не зависит от обобщенных констант. Т.е. для составления критериального уравнения необходимо в исходном уравнении исследуемой модели заменить обобщенные константы на критерии подобия, а параметры и затраты – их относительными величинами.

 Критериальное уравнение (1.35) позволяет исследовать экономическую устойчивость затрат к отклонению параметра от экономических значений.

Решая уравнение

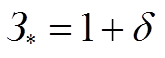 (1.36),

где d = 0.05 – нормированное увеличение затрат по сравнению с экономическим значением.

Можно определить допустимые относительные отклонения оптимизируемых параметров, соответствующие принятой зоне равноэкономичности.

Для исследования экономической устойчивости, исходя из (1.35) рассчитаем таблицу:

Таблица 1.1

Расчетные данные для исследования устойчивости

n*,о.е	0,63	0,65	0,7	0,8	0,9	1	1,2	1,3	1,4	1,5	1,53	1,55
З*,о.е	1,05	1,043	1,03	1,012	1,003	1	1,008	1,018	1,03	1,044	1,049	1,052

      З*,о.е.          

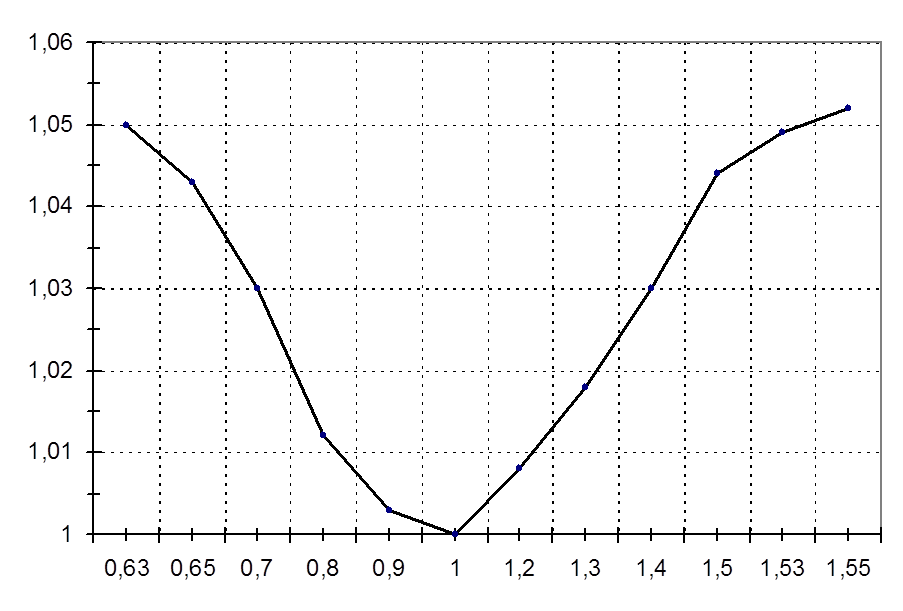
Рис. 1.2. Кривая экономической устойчивости

Исходя из таблицы 1.1 и рис. 1.2 допустимые отклонения оптимизируемого параметра от 0.63 до 1.54, т.е. данная модель является экономически устойчивой к изменению оптимизируемого параметра.

Четвертая задача технико-экономического анализа решается с использованием уравнений (1.26.1) и (1.27). Выражая обобщенные константы в долях от произвольно выбранных базисных значений Авб и Анб и получаем формулы для исследования чувствительности:

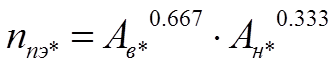 (1.37)

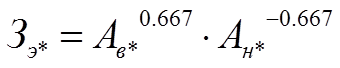 (1.38),

где

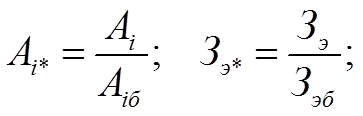
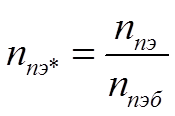   (1.39)

Исследования чувствительности проводится в о.е. и не требует знания обобщенных констант, т.е. исходных данных. Для исследования чувствительности будем задаваться парами значений обобщенных констант и, исходя из (1.37) и (1.38) рассчитаем таблицу и построим кривые чувствительности.

Таблица 1.2

Расчетные данные для исследования чувствительности