Транзисторные умножители частоты, страница 4

где B_2n — член, связанный с указанной 2n-й гармоникой. Как и в пентодном УЧ, величина его сравнительно мала, поэтому ниже его будем отбрасывать. Тогда первое слагае­мое в круглых скобках можно назвать выходной активной проводимостью транзистора, а второе - выходной емкост­ной проводимостью. Саму же выходную проводимость и емкость после вычисления интеграла для Х_п оказывается возможным записать в виде

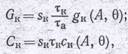                                                      (1.78)

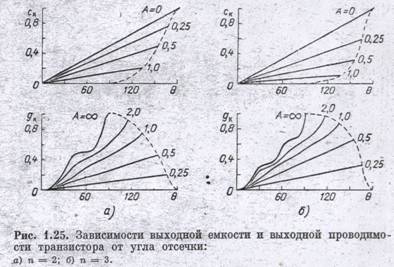
где g_K и с_к — безразмерные функции угла отсечки и пара­метра инерционности. Графики этих функций показаны на рис. 1.25. Обратим внимание на то, что как выходная проводимость, так и емкость оказываются зависящими от номера выделяемой гармоники. Как видно из рисунка, выходная емкость с ростом частоты падает, а проводимость возрастает. На низких частотах (А = 0) выходная прово­димость равна нулю. Получается так потому, что в эквива­лентной схеме транзистора на рис. 1.23 была отброшена проводимость, шунтирующая емкость С_кп. Практически, конечно, проводимость не равна нулю. Однако она очень мала и ею можно пренебречь.

Интересно определить величину «начальной» выходной емкости транзистора, т. е. величину нормировочного коэф­фициента в (1.78). Эта «начальная» емкость равна s_кτ_к = s_кr_sC_кп. Она больше емкости С_кп (рис. 1.23) в s_кr_s раз. Чтобы оценить величину этого произведения, надо сравнить точное и приближенное выражения для статической характеристики тока коллектора (1.74), (1.75). Из этого сравнения видно, что . Причем неравен­ство обращается в равенство в «существенно» активной области, когда последнее слагаемое, пропорциональное i_к преобладает в левых частях (1.74) и (1.75). В остальных случаях произведение несколько меньше β но имеет тот же порядок, т. е. много больше единицы. Это означает, что начальная выходная емкость транзистора оказывается много больше емкости С_кп. Правда, как видно из рис. 1.25, с ростом частоты эта емкость весьма быстро падает.

Перейдем теперь к расчету параметров входной цепи транзисторов. Как видно из рис. 1.23, первая гармоника базового тока транзистора, определяющая его входное сопротивление:

где U_п1 — первая гармоника напряжения на переходе. Используя уравнение (1.72), ее можно выразить через первую гармонику генератора тока коллектора. Проведя гармонический анализ обеих частей (1.72), можно записать

и, подставив в предыдущее уравнение, получить

                                         (1.79)

Поскольку при расчетах коллекторного тока принима­лось, что на всех частотах в рабочем диапазоне , то эту величину в знаменателе (1.79) можно отбросить. В этом случае первое слагаемое дает ток, текущий через емкости С_э+С_кп, которые характеризуют входную цепь, когда транзистор заперт. Поскольку часть времени транзистор отперт, то в (1.79) появляется второе слагаемое, характе­ризующее ток, протекающий через емкость С_д и проводи­мость g_n. Подставляя сюда первую-гармонику коллектор­ного тока в виде (1.77), формулу (1.79) можно записать в виде