Транзисторные умножители частоты, страница 3

Такая аппроксимация сравнительно хорошо совпадает со статической характеристикой, если значения тока не слишком малы. В противном случае необходимо приме­нять другие аппроксимации, а расчеты становятся много сложнее.

Для решения уравнения (1.73) в него подставляется (1.75), а также синусоидальные напряжения на базе и кол­лекторе. Далее вводится косинус угла отсечки (1.12), а вели­чина тока нормируется

В этом случае для безразмерного тока х(τ) получается

                                 (1.76)

Здесь А —параметр инерционности транзистора:

ε  - параметр, учитывающий реакцию коллекторного напря­жения на ток коллектора:

 

Обычно этот параметр является малым, поскольку посто­янная времени коллекторной цепи меньше, чем постоянная времени транзистора в пассивной области. Это значит, что для рабочих частот  и потому , несмотря на то, что U_к> U_б.

Учитывая малость ε, решение (1.76) можно представить в виде ряда по его степеням, ограничиваясь линейным членом

Подставляя этот ряд в (1.76), можно получить два уравнения:

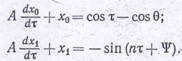
Решение первого из этих уравнений позволяет опреде­лить форму импульсов коллекторного тока при отсутствии реакции анода. Существенным является то, что импульс тока оказывается перекошенным. Передний фронт его затянут, а задний более крутой, чем у косинусоидального импульса. Запирание транзистора происходит при угле отсечки θ_з большем, чем угол отсечки θ. Поскольку импульс тока не симметричен, то его следует разложить в комплексный ряд Фурье. Каждая гармоника тока может быть записана в виде

                                                (1.77)

где комплексный коэффициент разложения

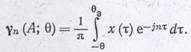
В случае низких частот (А = 0) коэффициент разложе­ния переходит в обычный при р = 1. С ростом частоты его модуль уменьшается и появляется фаза, зависящая от угла отсечки. Графики, отражающие эти зависимости для второй и третьей гармоник и необходимые для расчета удвоителя и утроителя, приведены на рис. 1.24.

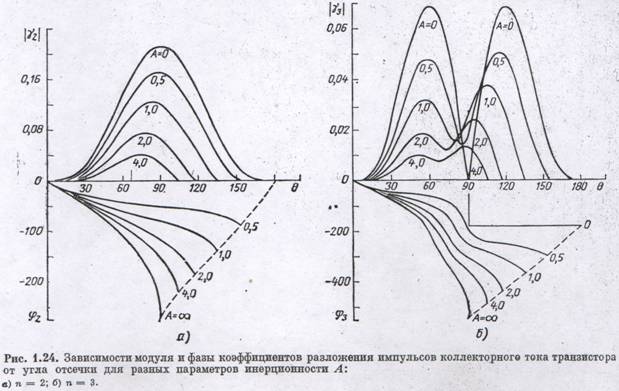
Из рисунка видно, что с ростом инерционности амплиту­ды гармоник уменьшаются и в результате уменьшается эффективность УЧ. Далее из рис. 1.24 видно, что фаза гармоник тока оказывается очень значительной и может достигать нескольких сот градусов. Фаза весьма сильно зависит от угла отсечки, т. е. от режима транзистора. Это значит, что УЧ на транзисторах обладает большой режим­ной нестабильностью фазы.

Перейдем к расчету дополнительного тока коллектора x₁(τ), связанного с учетом реакции коллекторного напря­жения. Мгновенное значение этого тока определяется в результате решения соответствующего уравнения. При вычислении гармоник этого дополнительного тока следует ввести компоненты, синфазную и квадратурную к напряже­нию на коллекторе. Первая из них характеризует выход­ную проводимость транзистора, а вторая — выходную емкость. Итак,

Здесь Х_п означает гармоники дополнительного тока

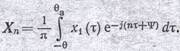
После вычисления интеграла оказывается, что он содер­жит член, зависящий от компексно-сопряженной амплитуды коллекторного напряжения. Очевидно, что это слагаемое связано с 2n-й гармоникой выходной проводимости так же, как это было в случае УЧ на пентоде (1.19). Это значит, что, строго говоря, дополнительный ток нельзя представить как ток, текущий через некоторые проводимость и емкость, а надо писать