Для расчета импульсов коллекторного тока (1.71) необходимо знать мгновенное значение напряжения на переходе. Считая все элементы эквивалентной схемы рис. 1.23 (кроме Сд и gп) постоянными, нетрудно составить дифференциальное уравнение, которому это напряжение удовлетворяет
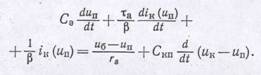
В левой части этого равенства представлен ток, вытекающий из перехода (точка «п» рис. 1.23) через емкость эмиттерного перехода, диффузионную емкость и проводимость gп соответственно. В правой части показан ток, втекающий в переход через сопротивление базы rs и емкость коллектор — переход Скп.
Собирая в левой части все величины, зависящие от напряжения на переходе, можно получить
![]() (1.72)
(1.72)
где τп = rs (Сэ + Скп) — постоянная времени транзистора в пассивном режиме, а τк = rsСкп — постоянная времени цепи коллектора.
Первая из них названа так потому, что она характеризует процессы в запертом транзисторе, когда iк= 0 и из (1.72) получается линейное дифференциальное уравнение для напряжения на переходе с постоянной времени τп.
В активной области, наоборот, мало напряжение на переходе, а ток генератора велик. Поэтому в (1.72) можно положить uп = 0 и получить для тока дифференциальное уравнение с постоянной времени τа.
К сожалению, транзисторы весьма редко работают в таких режимах, когда две указанные линейные области ярко выражены. В большинстве случаев в правой части (1.72) надо учитывать обе группы членов. Во всяком случае необходимо учитывать напряжение на переходе ип, имеющее тот же порядок, что и напряжение rsiкβ-1, пропорциональное току генератора. В то же время производной напряжения на переходе обычно можно пренебречь. Дело в том, что в (1.72) перед производными стоят постоянные времени τп и τа соответственно. Отношение же постоянных времени пассивной и активной областей является для транзисторов малой величиной. Для диффузионных транзисторов оно имеет порядок 10-3—10-2. Для высокочастотных дрейфовых транзисторов это отношение не больше 0,1—0,2. Все сказанное означает, что в (1.72) можно положить τп = 0, хотя для дрейфовых транзисторов такое предположение может давать заметную погрешность. В результате вместо (1.72) получается следующее уравнение:
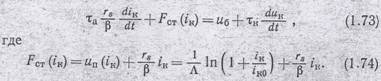
Полагая в (1.73) напряжения и токи неизменными во времени, убеждаемся, что функция Fст(iк) является обратной по отношению к статической зависимости тока коллектора от напряжения на базе. Статическая характеристика реального транзистора хорошо подчиняется закону (1.74) при соответствующем подборе параметров rs, β, iк0.
К сожалению, точное решение уравнений (1.73) и (1.74) невозможно. Приближенное решение численными методами наталкивается на трудности, связанные с тем, что необходимо найти стационарное решение, начальные условия для которого неизвестны. Конечно, подбирая начальные условия, это решение найти можно, однако ценность его для вычисления гармоник тока все равно невелика, поскольку оно зависит от большого числа параметров.
Чтобы обойти указанные трудности, аппроксимируем статическую характеристику коллекторного тока кусками прямых. Очевидно, что функция, обратная статической характеристике, в этом случае равна
![]() (1.75)
(1.75)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.