10
Эксперементальные основания СТО. Постулаты Эйнштейна. Пространство время и СО в СТО. Преобразовния Лоренца и их кинематические следствия.
В
Кл.Мех. при переходе из одной ИСО к др. ИСО (К®К’), К’
движется относительно К со скоростью ![]() . $
преобразования Галилея соответственно которым скорость точки m, в
ИСО равна
. $
преобразования Галилея соответственно которым скорость точки m, в
ИСО равна ![]() =
=![]() ’+
’+![]() - теорема о сложении скоростей.
- теорема о сложении скоростей.
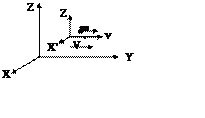 Возникли затруднения к применению з-ов
Мех. К распространению света. Если источник и приемник света движутся др.
относительно др. равномерно и прямолинейно то по Ньютону измеренная скорость
света далжна зависить от относительной скорости их движения.
Возникли затруднения к применению з-ов
Мех. К распространению света. Если источник и приемник света движутся др.
относительно др. равномерно и прямолинейно то по Ньютону измеренная скорость
света далжна зависить от относительной скорости их движения.
Опыт Майкельсона стал основанием СТО. Он использовал интерферометр устроеный следующим образом:
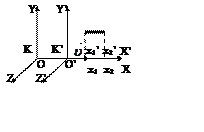
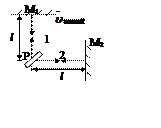 На
массивной плите установлен интерферометр. Полупрозрачное зеркало P,
зеркала М1 и М2. Пусть плечо PM2
На
массивной плите установлен интерферометр. Полупрозрачное зеркало P,
зеркала М1 и М2. Пусть плечо PM2![]() земли. Время необходимое лучу 1
чтобы пройти расстояние до М1 будет отлично от времяни необходимого для прохождения
пути РМ2Р лучом 2 Þ даже при равенстве плеч м/д
лучом 1 и 2 возникает разность хода, если повернуть прибор на 900,
плечи поменяются местами и разность хода поменяется тоже. Это должно было превсти
к смещению интерференционной картины на велечину которую можно было обнаружить.
По расчетам Майкельсона смещение должно было »0,4 полосы, а
интерферометр позволял измерить смещение порядка »0,01 полосы. Но
Майкельсон не обнаружил смещения полосы Þ эфирный ветер
неудалось обнаружить.
земли. Время необходимое лучу 1
чтобы пройти расстояние до М1 будет отлично от времяни необходимого для прохождения
пути РМ2Р лучом 2 Þ даже при равенстве плеч м/д
лучом 1 и 2 возникает разность хода, если повернуть прибор на 900,
плечи поменяются местами и разность хода поменяется тоже. Это должно было превсти
к смещению интерференционной картины на велечину которую можно было обнаружить.
По расчетам Майкельсона смещение должно было »0,4 полосы, а
интерферометр позволял измерить смещение порядка »0,01 полосы. Но
Майкельсон не обнаружил смещения полосы Þ эфирный ветер
неудалось обнаружить.
Эйнштейн смог объяснить накопившиеся факты и опыт Майкельсона. Он пришел к выводу что нет среды которая могла служить абсолютной системой отсчета. Он распространил принцип относительности Галилея на все без исключения физические явления. Принцип Относительности Эйнштейна – все законы природы инвариантны по отношению к переходу из одной ИСО к другой (состояние пр/лин равномер дв-я не оказывает влияние ни на какие физ явления), все ИСО равноправны.
Согласно ПОЭ - законы Ньютона и ур-я Максвелла сохраняют свою форму. Т.е при преобразовании ур-ий Максвела при переходе из одной ИСО в др. должны получатся ур-я того же вида.
Правила
Галилея не изменяют вид 2 з-н Ньютона но изменяют вид ур-ий Максвелла. Это
связано с тем, что в Кл.Мех. взаимодействие прередовалось ¥
большой скоростью. Но на самом деле ЭД показала конечность скоростипередачи
эл/маг взаимодействия: 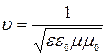 - в среде;
- в среде; 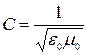 - скорость света в вакууме.
- скорость света в вакууме.
Гравитационное взаимодействие тоже передается со скоростью света в вакууме (предельная).
Т.е. СТО справедлива т.к. $ предельная скорость передачи сигнала, одинаковая во всех ИСО.
Постулат Эйнштейна – скорость света в пустоте одинакова во всех ИСО и не зависит от движения источника и приемника света.
Преобразования
Галлилея: 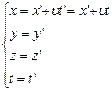 ÞVx=V’x+υ, Vy=V’y, Vz=V’z;Þ что если скорость света в К’ равна С, то в СО К
скорость света равнв (С+υ) – что неверно!Þ нужны другие
преоббразования.
ÞVx=V’x+υ, Vy=V’y, Vz=V’z;Þ что если скорость света в К’ равна С, то в СО К
скорость света равнв (С+υ) – что неверно!Þ нужны другие
преоббразования.
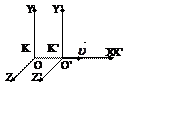 Оy, O’y’ – совпадают
Оy, O’y’ – совпадают
Оz,O’z’ – совпадают
Из однородности пространства следует, что формулы недолжны изменятся при переходе начала координат x®x+a Þy=εy’, т.к. К и К’ равноправны Þy’=εy Þ ε2=1 Þ ε=±1: 1) +1®yy’ 2)-1®y¯y’.
ε=+1 Þ аналогично для Z получаем![]() .
.
Рассмотрим
преобразования для t и x. (.)
О имеет координаты x=0 в СО К и x’=-υt в К’ Þ если x’+υt=0 то
и x=0 Þ т.е. линейное преобразование должно иметь вид: x=γ(x’+υt’).
Аналогично для (.) О’: x’=γ(x+υt)
(*). Т.к. К и К’ – равноправны то Þ
γ должна быть одна и таже: 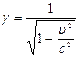 .
.
Преобразование времяни получается путем исключения x из уравнений (*), и получится: t=γ[t’+(x’/υ)(1-1/γ2)].
Т.о. получится система прямых и обратных пробразований Лоренца:
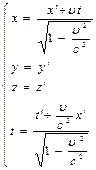
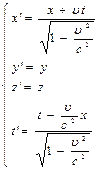
Следствия преобразований Л.:
] стержень расположен вдоль оси x и покоится отн-но К’. Его длина в этой системе ℓ0=x2’+x1’, x1’ и x2’ со временем не изменяются.
Относительно СО К стержень движется со скоростью υ. Для определения координат стержня в СО К необходимо отметить координаты его концов в один и тот же момнт времяни: t1=t2=t0. Разность ℓ=x2-x1 даст длину стержня в К.
x1’=γ(x1-υt0), x2’=γ(x2-υt0) Þ x2’-x1’= γ(x2-υt0)-γ(x1-υt0)=γ(x2-x1), x2-x1=(x2’-x1’)/γ. Þ ℓ=ℓ0/γ, ℓ<ℓ0. Относительно осей y и z размеры не меняются.
Промежуток времяеи м/д событиями:
] в СО К в (.) с координатами x1 и x2 происходит одновременно 2 события t1=t2=t0. Согласно преобразованиям Лоркнца в СО К’ этим событиям будут соответсвовать координаты x1’=γ(x1-υt0), x2’=γ(x2-υt0) и моменты времяни t1’=γ[t0-(υ/c2)x1], t2’=γ[t0-(υ/c2)x2].
Если x1=x2 Þ x1’=x2’. Если x1¹x2 – события пространственноно разобщены, Þ x1’=x2’ в К’ тоже разобщены. И при этом они не будут одновременными t1’¹t2’. Знак (t2-t1) определяется знаком в пространстве υ(x2-x1) Þ в различных СО (при разных υ) разность (t2’-t1’) будет различна по величене и знаку. Þ в одной СО событие 1 будет предшествовать событию 2 в другой СО (и наоборот) если м/д собой неимеются причиноследственые связи.
Преобразования скоростей:
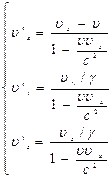
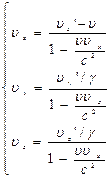
Собственное время – время м/д событиями находящихся в одной точке.
dτ-собственное время, ds-интервал м/д событиями: dτ=(i/c)ds.
Согласно
преобразованиям Лоренца координаты и время связаны м/д собой, поэтому удобно
записать постулаты Эйнштейна в виде инвариантности игтервала м/д событиями: 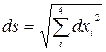 - интервал м/д событиями
- интервал м/д событиями
ds=inv, ds’=ds постоянная Эйнштейна.
x1=x, x2=y, x3=z, x4=ict – 4пространства-времяни Минковского. (пространство Минковского – xyz + координата отвечающая за время ict)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.