20
При
экспериментальном исследовании обнаруживается электромагнитное поле по его
силовым действиям, при котором энергия поля превращается в какую-либо другую
формы энергии. Полная энергия ЭМП является суммой электрической и магнитной
энергий и выражается из формул: 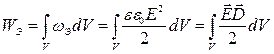 - энергия
электростатического поля.
- энергия
электростатического поля.
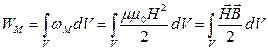 - магнитная энергия.
- магнитная энергия.
Как
![]() . Для плотности полная энергия ЭМП имеем:
. Для плотности полная энергия ЭМП имеем: ![]() . ЭМП может переносить электромагнитную
энергию (поток энергии). Вычислим поток электромагнитной энергии в однородной
среде, исходя из уравнений Максвелла:
. ЭМП может переносить электромагнитную
энергию (поток энергии). Вычислим поток электромагнитной энергии в однородной
среде, исходя из уравнений Максвелла:
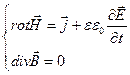 - система уравнений стационарного
магнитного поля.
- система уравнений стационарного
магнитного поля.
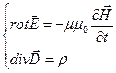 - система уравнений электростатического
поля.
- система уравнений электростатического
поля.
 Для
этого умножим обе стороны 1 уравнения скалярно на
Для
этого умножим обе стороны 1 уравнения скалярно на ![]() , а обе
стороны 2 уравнения на
, а обе
стороны 2 уравнения на ![]() :
: ![]() ,
, ![]() (1).
В соответствии с законом Ома:
(1).
В соответствии с законом Ома:![]() получим:
получим: ![]() и
и 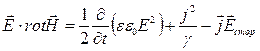 (2). Используем формулу векторного анализа:
(2). Используем формулу векторного анализа:
![]() . И в соответствии с ней вычтем из (1) (2):
. И в соответствии с ней вычтем из (1) (2):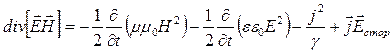 . Перепишем это выражение:
. Перепишем это выражение: 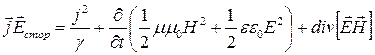 (3). Это выражение представляет собой
наиболее общую запись закона сохранения энергии электромагнитного поля в
дифференциальной форме. Рассмотрим физический смысл отдельных величин входящих
в него. Произведение
(3). Это выражение представляет собой
наиболее общую запись закона сохранения энергии электромагнитного поля в
дифференциальной форме. Рассмотрим физический смысл отдельных величин входящих
в него. Произведение ![]() - работа сторонних ЭДС в единицы
объема за единицу времени, то есть мощность; частное
- работа сторонних ЭДС в единицы
объема за единицу времени, то есть мощность; частное ![]() -
джоулева теплота, выделенная в единицу объема за единицу времени; частная
производная
-
джоулева теплота, выделенная в единицу объема за единицу времени; частная
производная ![]() - приращение электромагнитной
энергии единицы объема за единицу времени, а
- приращение электромагнитной
энергии единицы объема за единицу времени, а ![]() - поток
энергии, вытекающий из единиц объема за единицу времени, следовательно, закон
читается так: в единице объема за единицу времени работа сторонних ЭДС идет
на покрытие джоулевых потерь, на увеличение электромагнитной энергии и на
покрытие убыли энергии, вытекающей наружу. Вектор
- поток
энергии, вытекающий из единиц объема за единицу времени, следовательно, закон
читается так: в единице объема за единицу времени работа сторонних ЭДС идет
на покрытие джоулевых потерь, на увеличение электромагнитной энергии и на
покрытие убыли энергии, вытекающей наружу. Вектор ![]() представляет
собой поток энергии, через единичную площадку, расположенную перпендикулярно
потоку. При
представляет
собой поток энергии, через единичную площадку, расположенную перпендикулярно
потоку. При ![]() и
и ![]() поток
постоянен и вектор
поток
постоянен и вектор ![]() выражает поток энергии за
единицу времени; при переменных
выражает поток энергии за
единицу времени; при переменных ![]() и
и ![]() он выражает мгновенное значение потока.
Введем обозначение:
он выражает мгновенное значение потока.
Введем обозначение: ![]() , где
, где ![]() -
называют вектором Умова-Пойтинга. Умножим (3) на элемент объема и
проинтегрируем по всему объему поля:
-
называют вектором Умова-Пойтинга. Умножим (3) на элемент объема и
проинтегрируем по всему объему поля: 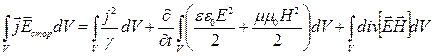 . После преобразования
последнего интеграла согласно формуле Остраградского-Гаусса получим:
. После преобразования
последнего интеграла согласно формуле Остраградского-Гаусса получим: 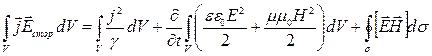 (4), где
(4), где ![]() -
поверхность. Здесь интеграл в левой части обозначает работу
-
поверхность. Здесь интеграл в левой части обозначает работу ![]() сторонних ЭДС в объеме, первый интеграл
справа – количество теплоты
сторонних ЭДС в объеме, первый интеграл
справа – количество теплоты ![]() , выделяющейся в этом
объеме, затем идет приращение энергии в этом объеме и поток электромагнитной
энергии через поверхность
, выделяющейся в этом
объеме, затем идет приращение энергии в этом объеме и поток электромагнитной
энергии через поверхность ![]() , ограничивающую
объемам. При постоянстве всех величин работа, теплота и так далее относится к
единице времени; в общем случае следует говорить о мгновенных значениях. Выражения
(4) – закон сохранения энергии в интегральной форме. С учетом введенных
обозначений он принимает вид:
, ограничивающую
объемам. При постоянстве всех величин работа, теплота и так далее относится к
единице времени; в общем случае следует говорить о мгновенных значениях. Выражения
(4) – закон сохранения энергии в интегральной форме. С учетом введенных
обозначений он принимает вид: 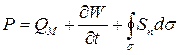 . Из выражения:
. Из выражения: ![]() , вытекает, вектор Умова-Пойтинга
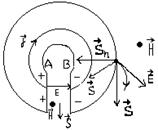
перпендикулярен этим векторам. Рассмотрим теперь поток энергии в цепи
постоянного тока. Работа сторонних сил совершается в источнике, из которого
энергия вытекает наружу; затем энергия перемещается вдоль проводника и извне
постепенно втекает в проводник, переходя здесь в джоулеву теплоту. Это
подтверждает направление вектора У.-П., показанное на рисунке . На участке АВ
(внутри источника) ток идет от В к А, а поле
, вытекает, вектор Умова-Пойтинга
перпендикулярен этим векторам. Рассмотрим теперь поток энергии в цепи
постоянного тока. Работа сторонних сил совершается в источнике, из которого
энергия вытекает наружу; затем энергия перемещается вдоль проводника и извне
постепенно втекает в проводник, переходя здесь в джоулеву теплоту. Это
подтверждает направление вектора У.-П., показанное на рисунке . На участке АВ
(внутри источника) ток идет от В к А, а поле ![]() направленно
от А к В. Следовательно, вектор У.-П. направлен из источника наружу. У
произвольной точки С, лежащей на поверхности проводника, электрический вектор
направлен по касательной к силовой линии: магнитный вектор обозначен точкой, то
есть направлен «на нас»; следовательно, вектор У.-П. направлен внутрь
проводника. Разлагаем его на две составляющие: нормальную
направленно
от А к В. Следовательно, вектор У.-П. направлен из источника наружу. У
произвольной точки С, лежащей на поверхности проводника, электрический вектор
направлен по касательной к силовой линии: магнитный вектор обозначен точкой, то
есть направлен «на нас»; следовательно, вектор У.-П. направлен внутрь
проводника. Разлагаем его на две составляющие: нормальную ![]() и тангенсальную
и тангенсальную ![]() .
Наличие обеих составляющих отражает тот факт, что энергия здесь частично
втекает в проводник, частично перемещается дальше вдоль проводника в
направлении тока. Теория Максвелла приводит к фундаментальному различию между
ролью проводников и непроводников в процессе передаче энергии. Неверно считать
заряды, являющиеся носителями тока, также и носителями электромагнитной энергии
тока. Носителем энергии является поле тока, локализованное как в проводнике, так
и в окружающем его пространстве; в проводнике происходит лишь поглощение
энергии, то есть ее превращение в другие виды энергии. Перейдем к рассмотрению
импульса электромагнитного поля. Пусть поле действует на объемные заряды,
распределенные в пространстве с плотностью
.
Наличие обеих составляющих отражает тот факт, что энергия здесь частично
втекает в проводник, частично перемещается дальше вдоль проводника в
направлении тока. Теория Максвелла приводит к фундаментальному различию между
ролью проводников и непроводников в процессе передаче энергии. Неверно считать
заряды, являющиеся носителями тока, также и носителями электромагнитной энергии
тока. Носителем энергии является поле тока, локализованное как в проводнике, так
и в окружающем его пространстве; в проводнике происходит лишь поглощение
энергии, то есть ее превращение в другие виды энергии. Перейдем к рассмотрению
импульса электромагнитного поля. Пусть поле действует на объемные заряды,
распределенные в пространстве с плотностью ![]() , и
токи с объемной плотностью
, и
токи с объемной плотностью ![]() . На заряды и токи
единичного объема действует сила:
. На заряды и токи
единичного объема действует сила: ![]() (1). Полная сила,
действующая на заряды и токи в объеме, выделенном в ЭМП, выразится интегралом:
(1). Полная сила,
действующая на заряды и токи в объеме, выделенном в ЭМП, выразится интегралом: ![]() (2). По теореме механики сила
(2). По теореме механики сила ![]() определяет изменение со временем импульса
определяет изменение со временем импульса ![]() всего вещества, заключенного в объеме
(учитывая при этом только силы электромагнитного происхождение):
всего вещества, заключенного в объеме
(учитывая при этом только силы электромагнитного происхождение): 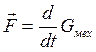 (3). Преобразуем (1), подставив
(3). Преобразуем (1), подставив ![]() и
и![]() их выражения из
уравнений Максвелла:
их выражения из
уравнений Максвелла: ![]() и
и 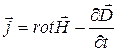 . В результате получим:
. В результате получим: 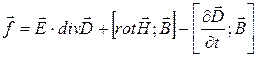 (4).
Принимая во внимание, что
(4).
Принимая во внимание, что ![]() , добавим к правой
части уравнения (4) равное нулю выражение
, добавим к правой
части уравнения (4) равное нулю выражение ![]() и
преобразуем последний член
и
преобразуем последний член 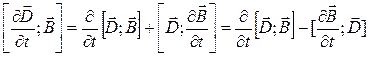 . Тогда
. Тогда
![]() (5). Составляющая сила
(5). Составляющая сила ![]() по оси равна:
по оси равна: ![]() ее
можно привести к виду:
ее
можно привести к виду: ![]() (6), где компоненты
(6), где компоненты ![]() выражаются так:
выражаются так: ![]() ,
,![]() . Введем в выражение (6) равенство
. Введем в выражение (6) равенство ![]() и перейдем к составляющей общей силы по
оси
и перейдем к составляющей общей силы по
оси ![]() :
: 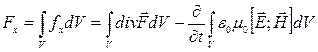 (7).
Составляющие по другим осям координат записываются аналогично. Заменим в (7)
силу
(7).
Составляющие по другим осям координат записываются аналогично. Заменим в (7)
силу ![]() ее выражением (3):
ее выражением (3): 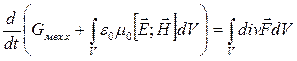 (8),
и преобразуем последний интеграл по формуле О.-Г. :
(8),
и преобразуем последний интеграл по формуле О.-Г. : ![]() . Он
представляет собой х-ю составляющую силы, действующей на поверхность,
охватывающую объем. Для других составляющих
. Он
представляет собой х-ю составляющую силы, действующей на поверхность,
охватывающую объем. Для других составляющих ![]() формулы
аналогичны. Переходя от составляющих к векторам, можно записать:
формулы
аналогичны. Переходя от составляющих к векторам, можно записать: 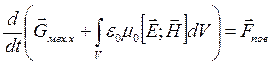 (9). Если на поверхность
(9). Если на поверхность ![]() , охватывающей объем, векторы
, охватывающей объем, векторы ![]() и
и ![]() =0, то
=0, то ![]() . Это условие выполняется, если поверхность
интегрирования
. Это условие выполняется, если поверхность
интегрирования ![]() бесконечно удалена, а все заряды
и токи локализованы в ограниченном объеме, образующем замкнутую систему. Тогда
бесконечно удалена, а все заряды
и токи локализованы в ограниченном объеме, образующем замкнутую систему. Тогда 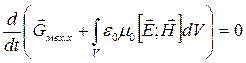 следовательно,
следовательно, 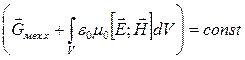 (10).
Таким образом при взаимодействии зарядов и токов в определенном объеме с ЭМП
сохраняется не импульс вещества, а его сумма с вектором
(10).
Таким образом при взаимодействии зарядов и токов в определенном объеме с ЭМП
сохраняется не импульс вещества, а его сумма с вектором 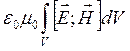 ,
который имеет размерность импульса. Этот интеграл выражает импульс ЭМП в
объеме V, а вектор
,
который имеет размерность импульса. Этот интеграл выражает импульс ЭМП в
объеме V, а вектор ![]() - его объемную плотность, соответственно:
- его объемную плотность, соответственно:
![]() (11). Очевидно в ЭМП сохраняется сумма
импульсов вещества и поля:
(11). Очевидно в ЭМП сохраняется сумма
импульсов вещества и поля: ![]() (12) следовательно, закон
сохранения импульса выполняется строго только, в том случае, когда наряду
с механическим импульсом
(12) следовательно, закон
сохранения импульса выполняется строго только, в том случае, когда наряду
с механическим импульсом ![]() вещества будет учтен и
импульс
вещества будет учтен и
импульс ![]() электромагнитного поля. Из ЗСИ вытекает,
что ЭМП при отражении или поглощении его телом оказывает на него давление (световое
давление). Если бы тело было свободном, то под действием световое давление
оно приобрело бы ускорение в направлении движении поля, то есть увеличился бы
его импульс. Приращение импульса одного тела связано с убылью импульса других
частей системы. В нашем случае убывает импульс ЭМП. Давление, оказываемое
электромагнитной волной на поглощающее тело, равно импульсу, передаваемому
волной мелу в единицу времени и на единицу поверхности. При падении волны по
нормали к поверхности и ее полном поглощении поверхностью, давление равно:
электромагнитного поля. Из ЗСИ вытекает,
что ЭМП при отражении или поглощении его телом оказывает на него давление (световое
давление). Если бы тело было свободном, то под действием световое давление
оно приобрело бы ускорение в направлении движении поля, то есть увеличился бы
его импульс. Приращение импульса одного тела связано с убылью импульса других
частей системы. В нашем случае убывает импульс ЭМП. Давление, оказываемое
электромагнитной волной на поглощающее тело, равно импульсу, передаваемому
волной мелу в единицу времени и на единицу поверхности. При падении волны по
нормали к поверхности и ее полном поглощении поверхностью, давление равно: 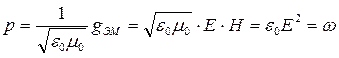 (13). В выражении (13)
(13). В выражении (13) ![]() - плотность электромагнитной энергии волны.
Следовательно, давление электромагнитной волны в этом случае численно равно
плотности энергии волны. В случае полного отражения от поверхности тела импульс
волны меняется на противоположный и поверхности тела передается импульс в 2
раза больший, чем при полном поглощении следовательно, и давление в этом
случае будет в 2 раза больше.
- плотность электромагнитной энергии волны.
Следовательно, давление электромагнитной волны в этом случае численно равно
плотности энергии волны. В случае полного отражения от поверхности тела импульс
волны меняется на противоположный и поверхности тела передается импульс в 2
раза больший, чем при полном поглощении следовательно, и давление в этом
случае будет в 2 раза больше. ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.