Энергия взаимодействия двух точечных одноименных заряда

Страницы работы

Фрагмент текста работы

Пусть q₁ и q₂ — два точечных одноименных заряда, расположенных на расстоянии r друг от друга в неограниченной однородной диэлектрической среде. Через φ₁₂ и φ₂₁ обозначим потенциалы поля в точках М₁ и М₂, в которых расположены эти заряды.

М₁ r М₂

q₁ q₂

φ₁₂ φ₂₁

При перемещении заряда q₂ из ∞ в точку М₂ внешние силы совершают работу: -А_∞ q₂ φ₁₂==W (заряд q₁ при этом фиксирован). Эта работа определяет потенциальную энергию заряда q₂ в точке М₂ . Величину +А∞ можно рассматривать как работу поля заряда q₁ по выталкиванию заряда q₂ на ∞ за счет потенциальной энергии W заряда q₂в поле заряда q₁. Таким же образом можно найти потенц. энергию заряда q₁ в точке М₁: –А∞ = q₁ φ₁₂ ==W. Здесь следует говорить об энергии взаимодействия обоих зарядов и потому выражение для W записывают в симметрич. форме:

W= (q₁φ₁₂ + q₂φ₂₁) (1)

В случае разноименных зарядов, т. е. при наличие сил притяжения, энергия взаимодействия имеет отрицательный знак.

Энергия взаимодействия системы из 3-х точеч. зарядов q₁, q₂, q₃ типа (1): W₁= (q₁φ₁₂ + q₂φ₂₁), W₂ = (q₂φ₂₃ + q₃φ₃₂), W₃= (q₃φ₁₃ + q₃φ₃₁). При сложении этих выражений получим: W = [(q₁(φ₁₂ + φ₁₃)+ q₂(φ₂₁ + φ₂₃)+ q₃(φ₃₁ + φ₃₂)], где в любой круглой скобке указан потенциал, создаваемый в данной точке двумя др. зарядами. Введя обозначение φ₁= φ₁₂+ φ₁₃ и т.д., имеем для трех зарядов W = 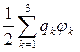. (2)

В случае же n зарядов: W = . (3)

В общем случае произвольного распределения зарядов разлагают общий заряд на совокупность элементарных объемных зарядов rdV и поверх-х зарядов sdS и применяют к ним формулу (3), переходя от суммирования к интегрированию

(4) где j - пот-л поля всех объемных и поверхностных зарядов в эл-те объема dV или на эл-те пов-ти dS.

Сообщенный проводнику заряд q распределяется по его поверхности так, чтобы напряженность поля внутри проводника была=0. Это справедливо лишь в том случае, если увеличение заряда на проводнике не вызовет изменений в распределении зарядов на окруж-х телах. Таким образо, различные по величине заряды распределяются на уединенном проводнике подоб. Образом, то есть отношение плотностей заряда в двух произв-х точках пов-ти проводника при любой величине заряда будет одно и то же. Þ, потенциал уединенного проводника пропорционален находящемуся на нем заряду. Действительно, увеличение в некоторое число раз заряда приводит к увеличению в то же число раз напряж-ти поля в любой точке окружающего проводник V₃. Þ, в такое же число раз увеличится работа переноса по любому пути единич. заряда из бесконечности на пов-ть проводника, то есть потенциал проводника. Таким образом, q = C×j (5)

Коэффициент пропорциональности С называется электроемкостью (емкостью) проводника. Емкость числ. = заряду, сообщение кот-го проводнику повышает его потенциал на единицу с = q/j. (6)

Вычислим потенциал заряженного шара радиуса R. Между разностью пот-лов и напряж-тью поля существует соотношение: j₁ - j₂ = 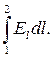Поэтому потенциал шара можно найти, проинтегрировав выражение по r от R до бесконечности (потенциал на бесконечности полагаем =0): . (7)

Сопоставив (7) и (6), находим, что емкость уедин. шара радиуса R, погруженного в однородный безграничный диэлектрик с относит. проницаемостью e : С = 4pe₀eR (8)

За единицу емкости принимают емкость такого проводника потенциал кот. изменяется на 18 при сообщении ему заряда в 1 кл. Эта единица емкости называется фарадой (ф).

Уединен. Проводники обладают малой емкостью. Даже шар таких размеров, как земля, имеет емкость ~ 700 мкф. Однако на практике бывает потребность в устройствах, кот. при небольшом отн-но окруж-х тел потенциале накапливали бы на себе («конденсировали») заметные по величине заряды. В основу таких устройств, называмых конденсаторами, положен тот факт, что емкость проводника возрастает при приближении к нему др. тел. Конд-ры делают в виде двух проводников, расположенных близко др. к др. Образующие конд-р проводники называют его обкладками. Чтобы внеш. тела не оказывали на ем-ть конд-ра, обкладкам придают такую форму и так располагают их др. отн-но др., чтобы поле создаваемое накапливаемыми на них зарядами было полностью сосредоточено внутри конд-ра. Этому условию удовлетворяют две пластинки, расположенные близко др. к др., два коаксиальных цилиндра и две концентрические сферы – плоские, цилиндрич. и сферические конд-ры. Под емкостью конд-ра понимается физич. величина, пропорциональная заряду q и обратнопроп. разности пот-лов между обкладками:

. (9)

Найдем ф-лу для емкости плоского конд-ра. Если площадь обкладки S, а заряд на ней q, то напряженность поля между обкладками = : Разность потенциалов между обкладками :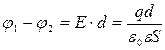, откуда для ем-ти плоского конд-ра получаем:

. (10)

S – площадь обкладки, d – величина зазора между обкладками, e - относит. диэлектрич. прониц-ть вещества, заполняющего зазор.

Выражение (4) может создать представление, что эл. эн. есть эн. Взаимодействия на расстоянии без учета промежуточной среды (дальнодействие). Такое представление исключает возмож-ть локализации эн. В промежуточной среде. Можно найти др. выражения для эн. вз-вия эл. зарядов, в кот. явно входит объем V₃, занимаемый полем. Найдем эн. уединен. заряженного проводника, имеющего потенциал j₀ в однородной среде. Эл. эн. проводника = работе против эл. сил отталкивания, затраченной при последовательном сообщении ему малых зарядов dq. Если заряды переносят из бесконечности, где по условию j_¥=0 (или Земли), то перенос любого элементарного заряда dq на тело сопряжен с работой.

-dA = jdq, где j - потенциал тела в соответствующий момент. Полная работа внеш. сил при зарядке тела равна: . Перепишем это выражение с учетом связи между пот-лом j, зарядом q и емкостью С проводника: q = Cj, dq = Cdj, откуда 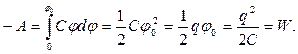(11)

Рассматривая аналогич. Образом процесс зарядки плоского конд-ра как перенос элементарных зарядов с одной его обкладки на др., получим для эн. заряженного конд-ра: или с учетом (9) и (10) и связи разности пот-лов с напряж-тью в однород. поле: имеем:.

Но dS = V- V₃, занимаемое полем. Таким образом, (12)

Появление объема в выражении для эн. вз-вия эл. зарядов имеет глубокий физ. смысл: эл. эн. локализована в V₃ , занимаемом эл. полем. В силу этого можно ввести понятие V-ной плот-ти эн-гии w: .(13)