Формирование свойств неразличимости систем одинаковых частиц

42

Свойство неразличимости систем одинаковых частиц формируется таким образом: в системах одинаковых микрочастиц возможны переходы которые ведут к экспериментальным неразличимым состояниям. Рассмотрим например соударение двух микрочастиц. Если бы даже в некоторый момент перед соударением частицы были локализованы любая отдельно от другой, в дальнейшем волновые пакеты, представляющие движения этих частиц, будут перекрываться и различие  частиц теряет смысл.

                  Пусть состояние системы в некоторый момент времени описывается волновой функцией Ψ(x₁,x₂): через х₁ обозначена совокупность всех координат одной частицы, а через х₂ – совокупность координат другой частицы. Введем оператор перестановки P, действие которого состоит в том, что он меняет местами частицы. Подействовав этим оператором на функцию Ψ(x₁,x₂), получим функцию, описывающую систему с переставленными одна на место другой частицами - Ψ (x₂,x₁). В силу принципа тождественности одинаковых частиц полученная система не отличается от исходной. Другими словами волновая функция РΨ(x₁,x₂) может отличаться от функции Ψ(x₁,x₂) только постоянным множителем РΨ(x₁,x₂)= Ψ(x₂,x₁)=αΨ(x₁,x₂)                      (1).

                  Действуя оператором второй раз мы придем к исходному состоянию

Р²Ψ(x₁,x₂)=РΨ(x₂,x₁)=РαΨ(x₁,x₂)= α²Ψ(x₁,x₂)=Ψ(x₁,x₂)                   (2).            Следовательно. Собственное значение оператора Р² есть α²=1, а собственное значение оператора Р : α= +- 1 следовательно, Ψ(x₁,x₂)=+- Ψ(x₂,x₁)                  (3).

                  Таким образом принцип тождественности одинаковых частиц ведет к определенному свойству симметрии волновой функции, так как при перестановке частиц волновая функция либо не меняет, либо меняет знак. Волновая функция которая не меняется при перестановке частиц, называется симметричной относительно этих частиц, а волновая функция, которая при перестановке частиц может менять свой знак, называется антисимметричной.

                  Мы рассмотрели функции координат частиц, характеризующих их положение в V₃. для полного описания состояния частиц необходимо учесть еще один параметр – проекцию спинового момента S_z.

                  Пусть система состоит из двух одинаковых частиц. Обозначив совокупность всех координат: пространственных и спиновых, соответственно цифрами 1 и 2, можно записать свойства функции 2-х частиц в виде равенств: Ψ_S(1,2)=U_S(2,1),  Ψ_A(1,2)=-U_A(2,1)

                  Пусть для простоты частицы между собой не взаимодействуют и состояние любой из частиц описывается функциями Ψ₁ и Ψ₂, следовательно функции системы частиц имеют вид: Ψ_S=        Ψ_A=            (4).

                  Антисимметричную функцию можно так же представить в виде определителя Ψ_А=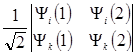

это остается в силе и для системы n тождественных частиц, состояние которой описывается произведением функции Ψ=Ψ_i(1)Ψ_k(2)… Ψ_р(n)(5).             Так как возможно всего n! перестановок,  следовательно можно построить n! функций вида (5), среди которых будет иметься одна симметричная и одна антисимметричная относительно координат любой пары частиц. Таким образом симметричная функция имеет вид: Ψ_S=  (6)

                  Антисимметричная функция 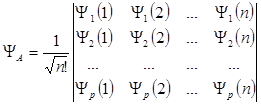        (9)

                  Оказывается, что в природе существует два типа частиц: одни, как например, фотоны, характеризуется тем, что их системы описываются симметричными функциями; другие, как например, электроны, протоны, нейтроны, описываются антисимметричными функциями. Частицы 1-го типа называются частицами Бозе, а частицы 2-го типа – частицами Ферми, по той причине, что к совокупностям 1-х применима статистика Бозе, а к совокупностям 2-х – статистика Ферми. Критерием по которому различаются эти частицы является их спин: частицы Бозе обладают целым спином (включая спин, = нулю), частицы Ферми – полуцелым (1/2, 3/2, …).