Движение электрона в скрещенных электрическом и магнитном полях в магнетроне. Определение удельного заряда электрона методом магнетрона

ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО ЗАРЯДА ЭЛЕКТРОНА МЕТОДОМ МАГНЕТРОНА

1.  Цель работы

            Изучить движение электрона в скрещенных электрическом и магнитном полях в магнетроне теоретически. Научиться точно вычислять магнитное поле на оси катушки данных размеров. Вывести формулу для определения удельного заряда электрона.

            Определить удельный заряд электрона методом магнетрона и оценить погрешность полученного результата.

2.  Теоретическое введение

А. Движение электрона в скрещенных электрическом и магнитном полях в магнетроне

            Магнетрон представляет собой вакуумный диод, катодом которого является накапливаемая электрическим током вольфрамовая нить, расположенная по оси медного цилиндра - анода. На рис.1 показано схематично расположение анода  и катода в магнетроне.

            Если между катодом и анодом магнетрона приложено напряжение (на аноде), то электроны, вылетающие из нагретой нити, будут двигаться в цилиндрически-симметричном электрическом поле вдоль силовых линий - радиусов (см. рис.2).

            Сила , приложенная к электрону, будет равна , где  - величина напряженности электрического поля на расстоянии  в цилиндрическом конденсаторе - анод. Радиус нити обозначим , радиус анода .

            Для вычисления можно воспользоваться четвертым уравнением Максвелла в интегральной форме (теоремой Остроградского-Гаусса).

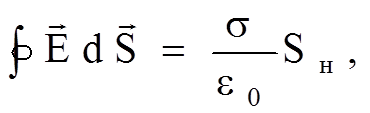
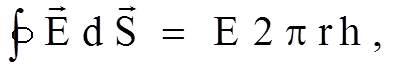
где    - боковая поверхность нити; - высота анода; - поверхностная плотность заряда нити. Так как  

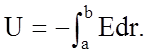
Поэтому

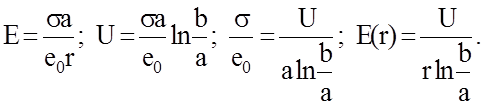                              (1)

            Вычислим для наших условий в нескольких точках.  , т.е. радиус нити  и радиус анода применяемого в аноде магнетрона. Результаты вычисления по формуле (1) представлены в таблице 1.

            Графически зависимость показана на рис.3.

Таблица 1

r (м)	a	b/10	b/2	b
E (кВ/см)	2,44	0,4	0,08	0,04

Таким образом, напряженность электрического поля  весьма велика на расстоянии от нити порядка нескольких радиусов , т.е. в малой области около нити. Электрон, вылетевший из нити, приобретает кинетическую энергию внутри этой области с сильным полем  и далее двигается в почти эквипотенциальном пространстве большую часть пути, т.е. с почти постоянной скоростью. Такое представление позволяет сделать приближенный расчет траектории электрона при наличии магнитного поля. Магнетрон помещается внутрь катушки (соленоида) так, что анод магнетрона находится в центре катушки около ее оси. Когда по соленоиду течет ток, внутри него создается магнитное поле. В центре достаточно длинного соленоида поле можно вычислить по формуле  или

                                          (2)

где - число витков на единицу длины соленоида; - ток в амперах;  Гн/м - магнитная постоянная вакуума; - напряженность магнитного поля в А/м. Направлено это поле вдоль оси катушки и совпадает с осью цилиндрического анода и с нитью лампы. Электрон, прошедший область сильного электрического поля и летящий к аноду с почти постоянной по величине скоростью под действием однородного магнитного поля будет двигаться по окружности. Радиус окружности подсчитаем, записав закон движения электрона:                ,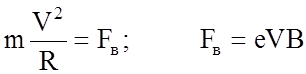

где m - масса электрона, F_В - сила Лоренца, В - индукция магнитного поля.

            Скорость  удобно подсчитать по закону сохранения энергии:

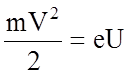
         Поэтому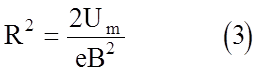                                  

Траектория электрона в магнетроне показана на рис. 4 и 5.

            Пусть теперь при неизменном потенциале анода U изменится ток в катушке (соленоиде). По мере увеличения тока будет расти магнитное поле В (см. формулу (3)) и уменьшаться радиус R. Как будет при этом изменяться анодный ток I_a в магнетроне? Легко видеть, что если 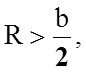 то все электроны, покинувшие катод, попадают на анод см. рис.4), т.е. I_a остается неизменным.Однако, при 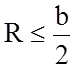 произойдет резкое уменьшение I_a, так как электроны начнут описывать полную окружность и не будут поглощаться анодом, как показано на рис.5.

            График зависимости I_a от В показан на рис.6.

            Момент, когда ток начинает резко падать, соответствует условию 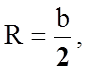а индукция B в этой точке называется критической индукцией B_кр. Подставим в формулу (3) эти значения и получим:

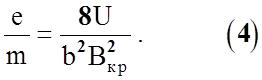
Таким образом, для определения необходимо определить B_кр при данном потенциале анода U.

            При выводе формулы (4) были приняты допущения, упрощающие ее получение.

            Можно не делать этих допущений и решить задачу о движении электрона в магнетроне более точно. Для этого запишем закон движения электрона в векторной форме: