![]() ,
(5)
,
(5)
где
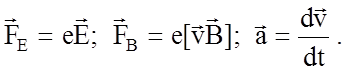
Спроектируем
уравнение на оси полярной системы координат r и ![]() с полюсом на оси z цилиндра и
полярной плоскостью, перпендикулярной этой оси.
с полюсом на оси z цилиндра и
полярной плоскостью, перпендикулярной этой оси.
Легко видеть, что
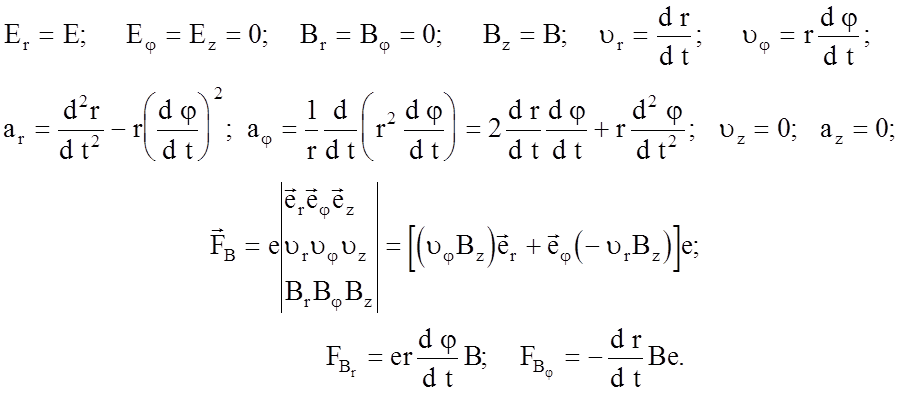
Подставляя
эти проекции в уравнение (5), получим систему дифференциальных уравнений:![]()
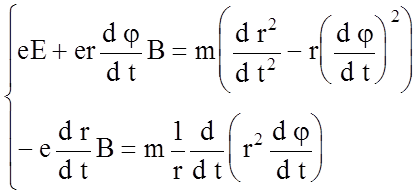 (6)
(6)
Второе уравнение преобразуем, учитывая, что
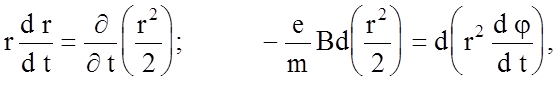
и после интегрирования
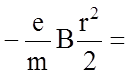
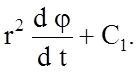
Считая, что электроны вылетают из нити перпендикулярно
ее поверхности, то есть 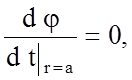
получим
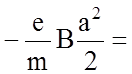
![]()
и
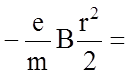
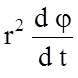
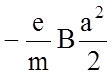 ;
; 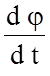
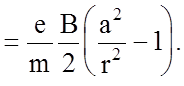
![]()
Полученное
значение  подставляем
в первое уравнение системы (6):
подставляем
в первое уравнение системы (6):
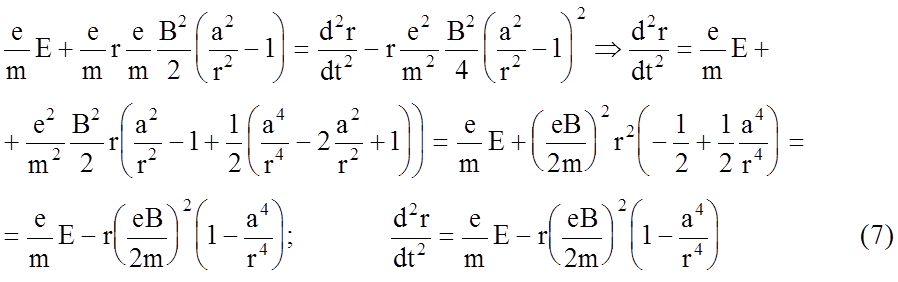
Производную преобразуем:
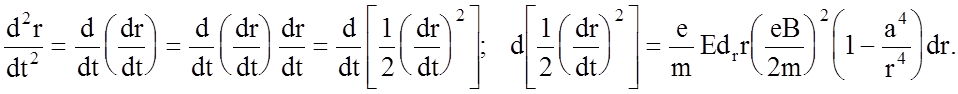
После интегрирования:
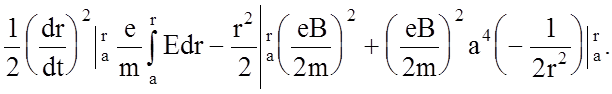
Учтем, что при
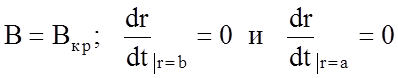 ,
,
т.е. электроны вылетают из нити с малой скоростью, тогда
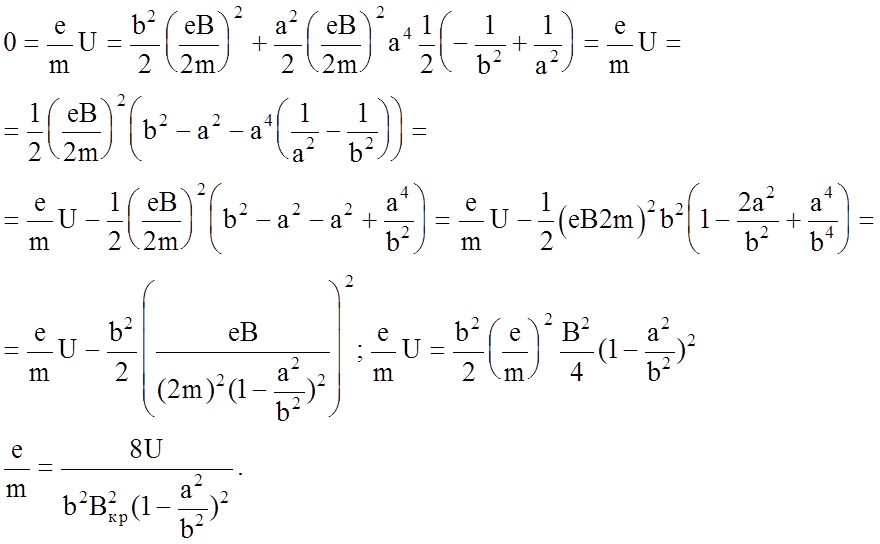 (8)
(8)
Формула (8) отличается от формулы (4) множителем
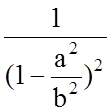 ,
,
что
для наших данных ![]() дает
дает
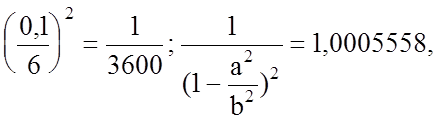
т.е. результат вычислений по приближенной (4) и по точной (8) формуле будет отличаться не более чем на 0,06 %.
В. Вычисление магнитного поля на оси катушки данных размеров
Формула (2) для вычисления B справедлива для достаточно длинного и тонкого соленоида (однослойного).
Если
![]() - высота, а
- высота, а ![]() и
и ![]() - радиусы внутренней и внешней обмотки
реальной катушки (см. рис.7), то условие применимости формулы (2)
- радиусы внутренней и внешней обмотки
реальной катушки (см. рис.7), то условие применимости формулы (2) ![]() и
и ![]() .
.
|
|
Можно более точно вычислить магнитное поле на оси катушки, воспользовавшись законом Био-Савара и Лапласа
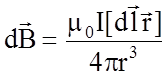 . (9)
. (9)
Здесь
![]() - индукция магнитного поля, созданная
элементом тока
- индукция магнитного поля, созданная
элементом тока ![]() , расположенном на расстоянии
, расположенном на расстоянии ![]() от оси катушки и на расстоянии
от оси катушки и на расстоянии ![]() от ее центра.
от ее центра. ![]() - радиус-вектор,
проведенный в точку M от элемента тока.
- радиус-вектор,
проведенный в точку M от элемента тока.
Введем
цилиндрическую систему координат с полюсом в точке O и перейдем к
непрерывному распределению тока по сечению катушки плоскостью, проходящей через
ось ![]() . Воспользуемся также очевидной для данной
задачи цилиндрической симметрией. Пусть
. Воспользуемся также очевидной для данной
задачи цилиндрической симметрией. Пусть ![]() - число
витков в слое (т.е. по h),
- число
витков в слое (т.е. по h), ![]() - число слоев (т.е.
число витков от
- число слоев (т.е.
число витков от ![]() до
до ![]() );
); 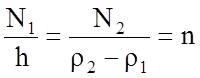 - плотность намотки (число витков на
единицу длины).
- плотность намотки (число витков на
единицу длины). ![]()
![]()
![]() - общее число витков.
- общее число витков.
Так
как ![]()
![]() , где
, где ![]() - объем элемента тока, равный
- объем элемента тока, равный ![]() - плотность тока, т.е. ток через единицу
сечения,
- плотность тока, т.е. ток через единицу
сечения, ![]() и
и ![]()
![]() ,
, ![]() , где
, где ![]() - полярный угол и
- полярный угол и
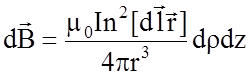
интегрируя, получим
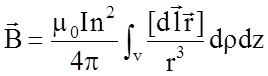 .
.
Вектор
![]() в точке
в точке ![]() направлен
вдоль оси
направлен
вдоль оси ![]() , так как ось
, так как ось ![]() является
осью симметрии, поэтому можно найти величину
является
осью симметрии, поэтому можно найти величину ![]() как
сумму проекций
как
сумму проекций ![]() на ось
на ось ![]() ;
;
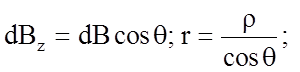
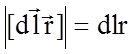 , так как всегда
, так как всегда ![]() .
.
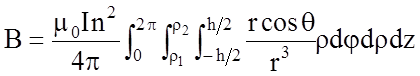 .
(10)
.
(10)
После
интегрирования по ![]() получим
получим
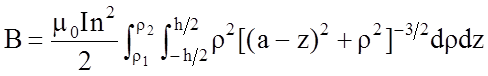 ,
,
где
![]() - расстояние от центра
- расстояние от центра ![]() до данной точки M по оси
до данной точки M по оси ![]() . Интегрируем по
. Интегрируем по ![]() от
от
![]() до
до ![]() .
Получим интеграл
.
Получим интеграл
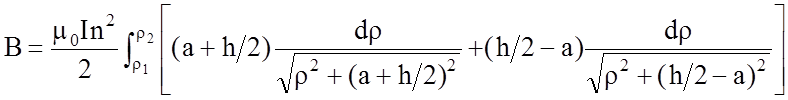 ,
,
который также берется:
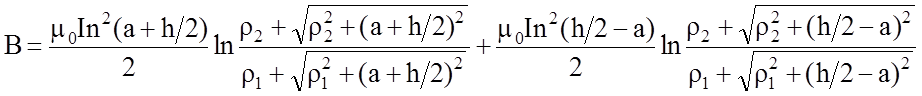 (11)
(11)
для центра катушки, т.е. в частном случае, когда a=0, получим
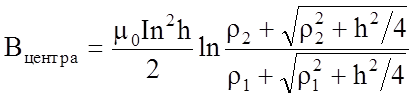 . (12)
. (12)
Магнитное поле на краю катушки (на торце) получится
при ![]() :
:
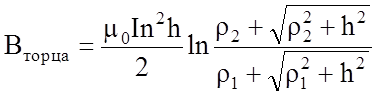 .
(13)
.
(13)
Формулы (11)-(13) позволяют с высокой степенью точности вычислить магнитное поле в любой точке на оси катушки конечных размеров. В нашем эксперименте анод и катод магнетрона помещается в центр катушки и поэтому можно пользоваться формулой (12).
Данные
катушки: ![]() витков.
витков.
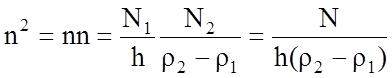 ,
,
поэтому
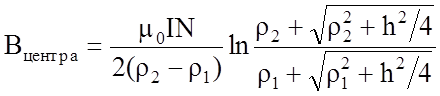 .
(14)
.
(14)
III. Оборудование
1. Магнетрон с медным анодом.
2. Микроамперметр 0-100 мкА.
3. Источник постоянных напряжений ИЭПП-2 ..
4. Стабилизатор тока накала магнетрона.
5а. Источник питания соленоида 0-400 мА; напряжение 0-600 В.
5б. Источник питания анода магнетрона УИП-1; выход 0-400 В.
6. Катушка-соленоид на подставке с магнетроном.
7. Миллиамперметр до 400 мА.
8. Соединительные проводники.
IV. Экспериментальная установка
|
|
|
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.