ИЗУЧЕНИЕ ПРОЦЕССА УПРУГИХ СОУДАРЕНИЙ ЭЛЕКТРОНОВ С АТОМАМИ ГАЗА В ПРИСУТСТВИИ ЭФФЕКТА РАМЗАУЭРА
Цель работы:
1. Экспериментальное изучение процесса упругого рассеяния электронов на атомах газа при их дрейфе в электрическом поле.
2. На основе экспериментальных данных определить энергии электронов, при которых рассеяние минимально и максимально.
Оборудование: лампа ТГ3-0,1/0,3; 2 батареи типа «Крона»; планшет для сборки; 2 вольтметра с пределом измерения до 20 B; микроамперметр с пределом измерения до 10 мкА; источник питания В4-12; ЛАТР.
Ведение
Одним из физических процессов, занимающих центральное место в физике плазмы и газовых разрядов и определяющих условия работы всех газоразрядных и плазменных приборов, является движение заряженных частиц (электронов и ионов) в газе. При этом происходят разнообразные столкновения с нейтральными частицами газа (атомами, молекулами).
Предметом рассмотрения этой работы является более частный вопрос — изучение особенностей процесса соударений электронов с атомами газа.
В зависимости от энергии электронов, различают упругие и неупругие столкновения. Упругие столкновения не сопровождаются изменением внутренней энергии атомов. Доля кинетической энергии, передаваемая при упругом столкновении электроном атому по порядку величины равна отношению
масс электрона и атома m/M ~ 10-4. Поэтому такое столкновение практически
не изменяет кинетическую энергию электрона, меняя лишь направление его движения. Упругие столкновения характерны для электронов с кинетической энергией до единиц эВ. Столкновения, в результате которых внутренняя энергия атома и кинетическая энергия электрона изменяются, называются неупругими. При неупругих столкновениях 1-рода электрон отдает часть своей энергии на возбуждение или ионизацию атома. В результате неупругих соударений 2-го рода электрону передается часть энергии возбуждения атома или вся эта энергия. Поэтому такого вида столкновения могут происходить лишь между электронами и атомами, находящимися в возбужденном состоянии. Неупругие столкновения 1-го рода происходят, если налетающие электроны имеют достаточную для возбуждения атома кинетическую энергию -десятки или сотни эВ.
Необходимость изучения рассматриваемого вопроса обусловлена целым рядом причин, из которых достаточно упомянуть только некоторые, откуда видна важность учета упругих столкновений электронов с атомами :
1) при прохождении электронных пучков через газ;
2) зависимость процессов транспорта в плазме (электропроводность, диффузия) от частоты упругих столкновений электронов с атомами;
3) формирование электронного энергетического спектра плазмы;
4) зависимость характера проявления контракции (сжатия) столба газоразрядной плазмы от частоты упругих соударений.
Столкновение электрона с одним атомом является случайным событием, имеющим определенную вероятность, которую можно характеризовать с помощью величины, называемой эффективным сечением рассеяния электрона Q. Атом рассматривается в виде шара с площадью поперечного сечения Q, численно равной вероятности столкновения электрона с атомом. Значение величины Qдля одного и того же атома различно для различных процессов, а для упругого рассеяния она выбирается такой, что при попадании в круг площадью Qэлектрон отклоняется от первоначального направления движения.
Когда электрон попадает на площадку S слоя толщиной dх газа с концентрацией атомов n0, в направлении движения электрона находится число
атомов, равное поSdх. При этом сумма поперечных сечений упругих столкновений электрона с атомами газа равна
![]()
Отсюда вероятность столкновения электрона с одним из атомов в слое dх равна
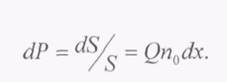
Эффективное сечение Qможно связать с экспериментально определенным коэффициентом ослабления μ электронного потока в газе. Поскольку ослабление электронного потока происходит за счет его рассеяния при столкновениях с атомами газа, то коэффициент μчисленно равен коэффициенту рассеяния потока электронов. Последний определяется как число столкновений электрона с атомами на единичной длине в газе. Поэтому при прохождении слоя dх величина рассеянной плотности потока электронов dIравна числу столкновений электронов пучка с атомами газа в этом слое :
![]()
Величина рассеянной плотности потока электронов, с другой стороны, определяется вероятностью упругих столкновений:
![]()
Сравнивая выражения (2) и (3), получаем
μ=Qn0
Плотность электронного потока 1(х) после прохождения слоя газа толщиной х связана с плотностью электронного потока на входе в газ I(0) соотношением
|
|
Отсюда, по данным измерения плотности электронного потока можно вычислить эффективное сечение рассеяния
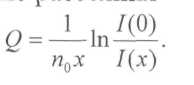
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.