Вычитание множеств. Дополнение множества.
Определение
Разностью множеств А и В называется множество, содержащее те и только те
элементы, которые принадлежат множеству А и не принадлежат множеству В.
Обозначается А \ В А
\ В = {x | x ![]() A и x
A и x ![]() B}
B}

 A
A
A B B![]() A,
A,
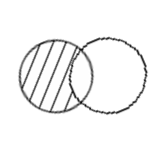
A \ B = B'А
![]()
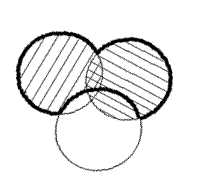
A \ B - заштрихованная область
Определение
Пусть В ![]() А. Дополнением множества В до множества А
называется множество, содержащее элементы множества А, которые не принадлежат
множеству В.
А. Дополнением множества В до множества А
называется множество, содержащее элементы множества А, которые не принадлежат
множеству В.
В'А = {
x | x ![]() A и х
A и х ![]() В,
В
В,
В![]() А}
А}
Как находить дополнение?
1) Если множества А,В заданы перечислением своих элементов. В дополнение В'А необходимо перечислить элементы, принадлежащие А и не принадлежащие В.
2) Если
множества А,В заданы характеристическими свойствами своих элементов и
В![]() А, то В'А задают характеристическим
свойством его элементов вида «
А, то В'А задают характеристическим
свойством его элементов вида «![]() и Х
и Х ![]() В»
В»
Пример:
А – множество четных чисел
В – множество чисел, кратных 4,
тогда множество В'А состоит из четных чисел, которые не делятся
на 4. 22 ![]() В'А ? Да
В'А ? Да
Выражение может включать
несколько действий над множествами: А\В![]() С
С
Внимание: пересечение ![]() более сильная операция, чем вычитание \ и
объединение
более сильная операция, чем вычитание \ и
объединение ![]() , а действия
, а действия ![]() и \ -
равноправные, выполняются согласно порядку записи в выражении
и \ -
равноправные, выполняются согласно порядку записи в выражении
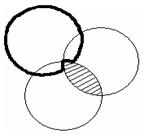
 Свойства вычитания: А
В
Свойства вычитания: А
В

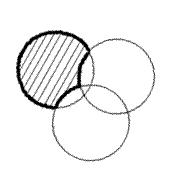 А
\ (В
А
\ (В Пример:
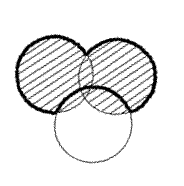 А В
А В
 А В С С
А В С С
Свойство 4
С С
Свойство 2
Декартово произведение множеств.
Из цифр 7 и 9 можно записать двузначные числа 79, 97, 99, 77. Записаны из одних цифр, но числа различные, важен порядок следования элементов, в математике говорят об упорядоченных наборах элементов, в данном случае – упорядоченная пара.
Из элементов а и в упорядоченная пара обозначается (а, в), где
а – первая координата (компонента)
в – вторая координата (компонента)
(а; в) = (с;d) тогда и только тогда когда а = с и в = d
Упорядоченные пары можно образовывать из элементов одного множества, двух множеств.
Пример:
Даны множества А = {1;2;3} и В = {3;5}. Образуем упорядоченные пары, где первая компонента принадлежит множеству А, а вторая принадлежит множеству В
(1;3); (1;5); (2;3); (2;5); (3;3); (3;5).
Получили множество упорядоченных пар, его называют декартовым
произведением, а обозначают А![]() В.
В.
Определение
Декартовым произведением множеств А и В называется множество всех упорядоченных пар, первая компонента которых принадлежит множеству А, а вторая компонента принадлежит множеству В.
А![]() В = { (х, у) | х
В = { (х, у) | х ![]() А и у
А и у ![]() В }
В }
Пример:
1) Найти А![]() В, если А = {m;p}, В = {e;f;k}
В, если А = {m;p}, В = {e;f;k}
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.