Определение общего числа возможных вариантов для разрабатываемого привода, страница 2

- используя значения передаточных отношений, определить числа зубьев всех зубчатых колес и диаметры шкивов ременных передач;

Составить уравнения кинематического баланса для всех частот вращения последнего вала и вычислить фактические значения оборотов;

- разработать и вычертить кинематическую схему для основного графика частот вращения.

Для заданного числа φ = 1,26 выписываем из таблиц рядов предпочтительных чисел проектные значения 12 - ти частот вращения от n_min до n_max:

80 - 100 - 125 - 160 - 200 - 250 - 315 - 400 - 500 - 630 - 800 - 1000

При выборе частоты вращении электродвигателя следует обеспечить минимальную степень редукции в приводе, поэтому согласно ряду значений частот односкоростных электродвигателей выбираем n_дв = 1000 об/мин с фактическим числом оборотов n_двфакт = 970 об/мин

Составление упрощенной структурной формулы

По исходному заданию возможно составление следующих структурных формул:

Z = 12 = 4*3 = 3*4 = 3*2*2 = 2*2*3 = 2*3*2

Для привода имеющего 3 группы, одна из которых на 3 передачи, остальные на 2 передачи, число возможных вариантов будет равно:

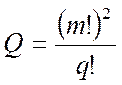
Где m – число групповых передач, q – число групп с одинаковым числом передач.

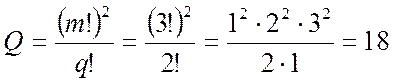 вариантов.

Учитывая также возможность создания привода из двух групп 12=4*3 с двумя возможными вариантами, полное число вариантов составит 20.

Из всех вариантов приводов с обычной множительной кинематической структурой, создающих одно и то же число скоростей на шпинделе станка предпочтение следует отдавать структурам с веерообразной сеткой, в которой группы с большим числом передач расположены ближе к электродвигателю. Нужно также стремиться к тому, чтобы первой в конструктивном порядке была основная группа, за ней следовала первая множительная, далее вторая множительная и т.д. так как это влияет на передаточные отношения привода. При такой последовательности сохраняется быстроходность промежуточных валов. Крутящие моменты на валах и окружные усилия на зубчатых колесах будут меньше, а, следовательно, меньшими окажутся изгибающие моменты и нагрузки на опорах,  что приведет к снижению металлоемкости и стоимости изготовления групповых передач. Поскольку диаметры валов и модули зубчатых колес обратно пропорциональны частоте  вращения вала или зубчатого колеса, то и габариты привода в этом случае будут меньше.

Исходя из этих рассуждений выберем вариант

Z = 12 =3*2*2

Упрощенная структурная формула для него запишется в виде:

Z = P₁ * P₂ * P₃ = 3 * 2 *2

Составление полной структурной формулы

Полная структурная формула запишется в виде:

Z = P₁(X1) * P₂(X2)  * P₃(X3)

Для выбранной конструкции привода общее число вариантов  кинематических структур привода (структурных сеток, графиков частот вращения, или полных структурных формул) определяется по формуле:

где m – число групповых передач в упрощенной структурной формуле;

Запишем эти варианты:

Z = 3(1) * 2(3) * 2(6)

Z = 3(1) * 2(6) * 2(3)

Z = 3(3) * 2(1) * 2(6)

Z = 3(6) * 2(1) * 2(3)

Z = 3(6) * 2(3) * 2(1)

Z = 3(3) * 2(6) * 2(1)

Согласно условию задания для анализа и сравнения кинематических свойств, выберем три полные структурные формулы и построим для них структурные сетки.

1) Z = 3(1) * 2(3) * 2(6);

2) Z = 3(2) * 2(1) * 2(6);

3) Z = 3(2) * 2(6) * 2(1).

Построим графики частот вращения.

Для построения трех графиков частот вращения строим соответствующее число заготовок для них в виде вертикальных линий – валов и сеток горизонтальных линий – частот вращения. Проводим  столько вертикальных линий, сколько валов в приводе. Для множительной структуры число валов NB равно числу механических групповых передач в структурной формуле, плюс 2 вала. Таким образом:

NB = 3 + 2 = 5.

Каждый вал, начиная с электродвигателя, обозначим римскими цифрами.