Контрольная работа №7
Вариант 9
Определение класса точности отливок.
Определить класс точности отливки типа вал, получаемый из сплава латуни ЛЦ 40С ГОСТ 17711-80 литьём под давлением.
Для анализа используется партия отливок из 30 штук. Измерен наружный диаметр D, который по чертежу имеет номинальный размер Dн = 60 мм. Измерения проводились с точностью до 0,01 мм. Данные замеров (вариант 9):
60,30; 59,50; 59,95; 60,15; 60,30; 60,10; 60,36; 59,90; 60,25; 60,00; 59,75; 60,00; 60,40; 60,45; 60,10; 59,65; 59,85; 59,95; 60,00; 60,50; 60,00; 59,70; 59,90; 59,90; 60,10; 60,10; 59,68; 59,75; 59,95; 59,85.
Решение.
По результатам измерений фактический размер D измеряется в пределах от 56,50 до 60,50 мм.
1. Ранжирую результаты замеров в табл.1. Получаю ряд размеров 56,50……60,45; 60,50.
Таблица 1.
|
№ п/п |
Замеры Di, мм |
Di – Dср, мм |
(Di – Dср)2, мм2 |
Частота m |
(Di – Dср)2· m, мм2 |
|
1 |
59,50 |
-0,51 |
0,2601 |
1 |
0,2601 |
|
2 |
59,65 |
-0,36 |
0,1296 |
1 |
0,1296 |
|
3 |
59,68 |
-0,33 |
0,1089 |
1 |
0,1089 |
|
4 |
59,70 |
-0,31 |
0,0961 |
1 |
0,0961 |
|
5 |
59,75 |
-0,26 |
0,0676 |
2 |
0,1352 |
|
6 |
59,85 |
-0,16 |
0,0256 |
2 |
0,0512 |
|
7 |
59,90 |
-0,11 |
0,0121 |
3 |
0,0363 |
|
8 |
59,95 |
-0,06 |
0,0036 |
3 |
0,0108 |
|
9 |
60,00 |
-0,01 |
0,0001 |
4 |
0,0004 |
|
10 |
60,10 |
0,09 |
0,0081 |
4 |
0,0324 |
|
11 |
60,15 |
0,14 |
0,0196 |
1 |
0,0196 |
|
12 |
60,25 |
0,24 |
0,0576 |
1 |
0,0576 |
|
13 |
60,30 |
0,29 |
0,0841 |
2 |
0,1682 |
|
14 |
60,36 |
0,35 |
0,1225 |
1 |
0,1225 |
|
15 |
60,40 |
0,39 |
0,1521 |
1 |
0,1521 |
|
16 |
60,45 |
0,44 |
0,1936 |
1 |
0,1936 |
|
17 |
60,50 |
0,49 |
0,2401 |
1 |
0,2401 |
2. Определяю среднее арифметическое значение измерений.
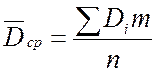 =60,01
мм.
=60,01
мм.
3. Вычисляю среднее квадратическое отклонение
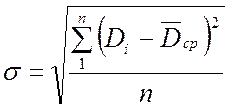 =
=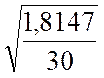 =0,246 мм;
=0,246 мм; ![]() мм.
мм.
4. Отбраковываем измерения с большой
погрешностью (проверю крайние значения ![]() =60,50 мм
и
=60,50 мм
и ![]() =59,50 мм).
=59,50 мм).
Оценку провожу по критерию Стьюдента.
Расчётное значение критерия ![]() для
для ![]() равно:
равно:
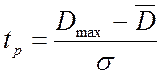 =
=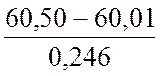 =1,992
=1,992
Табличное значение критерия ![]() (приложение табл.П1) для числа измерений п=30
и доверительной вероятности 0,95 составляет 2,0423. Следовательно
(приложение табл.П1) для числа измерений п=30
и доверительной вероятности 0,95 составляет 2,0423. Следовательно ![]() <
<![]() и
и ![]() =60,50 мм, следует оставить в выборке.
=60,50 мм, следует оставить в выборке.
Аналогично проверяю ![]() =59,50 мм:
=59,50 мм:
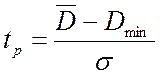 =
=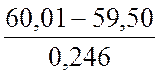 =2,0732.
=2,0732.
Табличное значение критерия ![]() (приложение табл.П1) для числа измерений п=30
и доверительной вероятности 0,95 составляет 2,0423. Следовательно
(приложение табл.П1) для числа измерений п=30
и доверительной вероятности 0,95 составляет 2,0423. Следовательно ![]() >
>![]() и
и ![]() =59,50 мм (одно измерение), следует считать
грубой ошибкой, которую необходимо отбросить.
=59,50 мм (одно измерение), следует считать
грубой ошибкой, которую необходимо отбросить.
Следующим крайним значением является
значение ![]() =59,65 мм, для которых
=59,65 мм, для которых ![]() равно соответственно 1,4634. Это значение
оставляем в выборке.
равно соответственно 1,4634. Это значение
оставляем в выборке.
В результате скорректированная выборка имеет 29 измерений, лежащих в пределах 59,65 – 60,50 мм.
5. Определяю среднее арифметическое значение измерений скорректированной выборки.
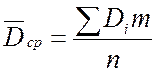 =
=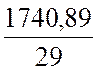 = 60,03 мм.
= 60,03 мм.
6. Вычисляю среднее квадратическое отклонение
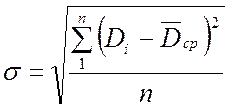 =
=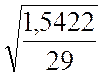 =0,23 мм;
=0,23 мм; ![]() мм.
мм.
7. Проверяю соответствие данной
выборки нормальному закону распределения. Для этого воспользуемся критерием
Пирсона ![]()
Расчёты оформляю в виде таблицы 2.
Все результаты измерений разбиваю на 6 интервалов.
7.1 Ширина интервала измерений:
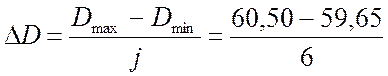 =0,14 мм.
=0,14 мм.
7.2 Результаты измерений представляю в виде интервального ряда с указанием границ каждого интервала.
Таблица 2
|
Интервал
|
|
|
|
|
|
|
|
|
|
59,79 |
5 |
0,1724 |
-1,04 |
-0,3485 |
0,1515 |
0,0837 |
|
59,79-59,93 |
59,93 |
5 |
0,1724 |
-0,43 |
-0,1664 |
0,1821 |
0,0149 |
|
59,93-60,07 |
60,07 |
7 |
0,2414 |
0,17 |
0,0675 |
0,2339 |
0,0069 |
|
60,07-60,21 |
60,21 |
5 |
0,1724 |
0,78 |
0,2793 |
0,2118 |
0,2124 |
|
60,21-60,35 |
60,35 |
3 |
0,1034 |
1,39 |
0,4177 |
0,1384 |
0,2560 |
|
|
+ |
4 |
0,1379 |
+ |
0,500 |
0,0823 |
1,0905 |
7.3 Относительная частота попаданий:
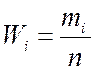
7.4 Нормирующий множитель для каждого интервала:
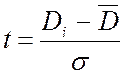
7.5 Для
каждого интервала по табл.П2 определяем интеграл вероятности ![]() .
.
7.6
Вероятность попадания в соответствующий интервал ![]() :
:
![]() =
=![]() -
-![]()
Сумма чисел последнего столбца даёт расчётное значение
критерия Пирсона: ![]() =1,6645
=1,6645
Сравниваем результат с табличным (приложение таблица П3).
Устанавливаем,
что для степени свободы ![]() при всех уровнях
доверительной вероятности Р от 0,95 до 0,999 выполняется неравенство
при всех уровнях
доверительной вероятности Р от 0,95 до 0,999 выполняется неравенство ![]() <
<![]() , где
, где ![]() =7,81…16,27,следовательно,
распределение размера D по принятым
интервалам соответствует нормальному закону.
=7,81…16,27,следовательно,
распределение размера D по принятым
интервалам соответствует нормальному закону.
8.
Вычисляем предельные отклонения анализируемого размера – поле допуска ![]() .
.
Примем ![]() равным полю рассеяния, величина которого
для нормального закона распределения при доверительной вероятности Р=0,997
равна
равным полю рассеяния, величина которого
для нормального закона распределения при доверительной вероятности Р=0,997
равна ![]() .
.
![]() =
=![]() =6∙0,23=1,38 мм.
=6∙0,23=1,38 мм.
Класс точности определяем по ГОСТ 26645-85. Для отливок с номинальным размером 40-63 мм допуск 1,38 мм соответствует девятому Т классу точности. Допуск на указанный интервал размеров отливок составляет не более 1,6 мм.
9. Предельные допустимые значения размеров отливки для вычисленного поля допуска составляют:
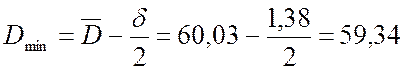 мм.
мм.
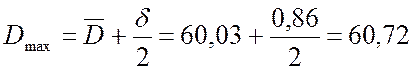 мм.
мм.
10. По данным таблицы 2 строю гистограмму и кривую распределения (рис.1).
СПИСОК ЛИТЕРАТУРЫ
Практикум по определению класса точности отливок:
Методические указания к выполнению ОргСРС по курсу «Технологические процессы в машиностроении» / Сост. Т.С.Тарасова Е.Ф.Уткин; Волгоград. гос.техн.ун-т – Волгоград, 2004.-29с.
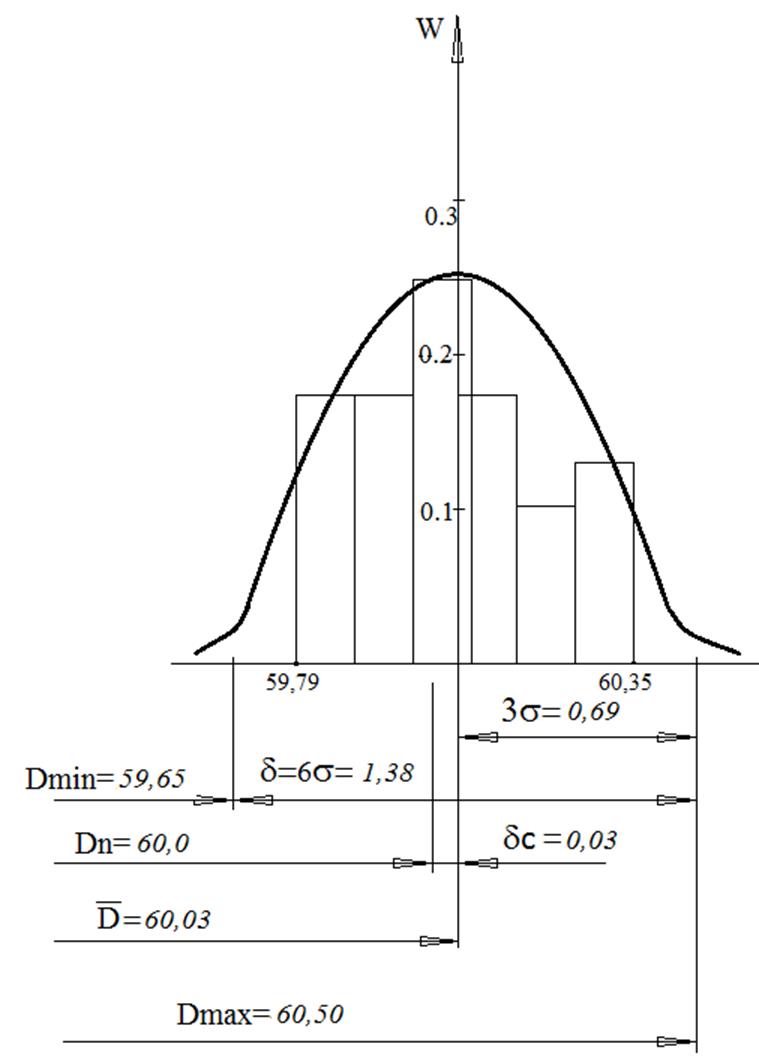
Рис.1
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.