Загальні принципи аналізу ризику. Відношення людей до ризику, страница 9

Втрата		Немає втрати
Сума, тис. грн.	Імовірність	Сума, тис. грн.	Імовірність
550	0,25	620	0,75

Відповідь. Очікувана вартість майна до придбання страхово­го полісу є середньозваженим двох можливих результатів, тобто 602,5 тис. грн. (550 · 0,25 + 620 · 0,75). Очікувана вартість майна після придбання страхового полісу дорівнюватиме різниці між су­мою, коли немає втрати, тобто 620 тис. грн., і вартістю страхово­го полісу. З нейтральної точки зору стосовно ризику очікувана вартість майна після придбання страхового полісу повинна бути не меншою, ніж у ситуації ризику, тобто поліс повинен коштувати не більше 17,5 тис. грн. (620-602,5). Противник ризику згоден сплатити навіть більшу суму.

12 Проблема вибору для інвестора

На підставі даних, наведених у табл. 4.18, записати рівнян­ня і побудувати графік бюджетної лінії. Показати криві байдужос­ті для вкладників, схильних до ризику, і противників ризику (схе­матично). Розрахувати ціну ризику. Для довільно взятої точки на бюджетній лінії розрахувати частку коштів, вкладених у ризикові активи. Розрахунки і побудови потрібно супроводжувати необ­хідними поясненнями.

Таблиця 4.18 - Вихідні дані

Норма прибутку за безризиковими активами, %	Норма прибутку за ризиковими активами, %	Стандартне відхилення очікуваної норми прибутку за ризиковими активами, %
2	12	21

Розгляньте теоретичну можливість збільшення норми прибутку за безризиковими активами до 25 %. Якщо, з вашого погляду, такі зміни не можливі, то поясніть, чому. У випадку, якщо вони можливі, опишіть, як змі­ниться ціна ризику (зменшиться чи збільшиться) та кут нахилу бюджетної лінії.

Відповідь. Рівняння бюджетної лінії має вигляд 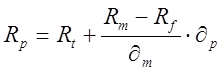, 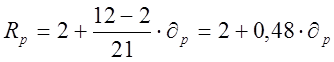. Графік бюджетної лінії побудовано на рис. 4.7.

Ціна ризику – додаткова норма прибутку, отримана при збільшенні ризику (стандартного відхилення) на одиницю, дорівнює (12-2)/21=0,48.

Для довільно взятої точки А  частка коштів, вкладених у ризикові активи, дорівнює 14/21=0,66 (66%). Відповідно в безризикові активи вкладено 34% коштів (1-0,66=0,34)

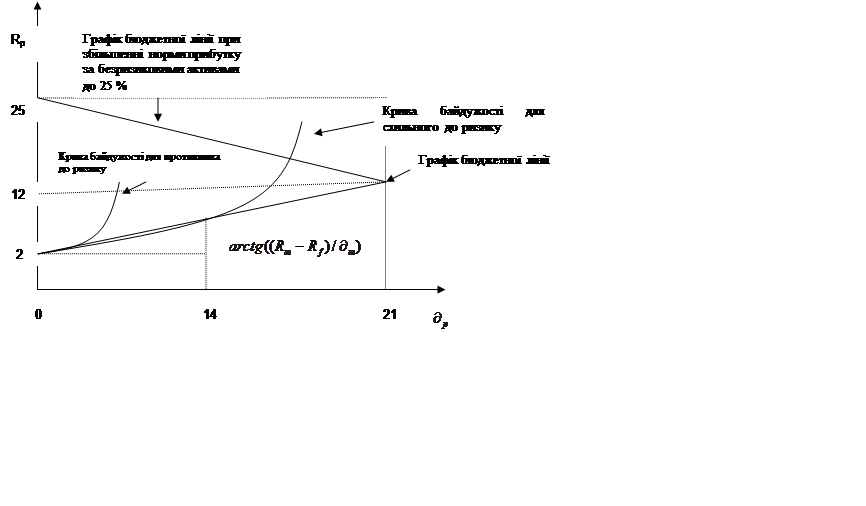
Рис. 4.7 - Графік бюджетної лінії

При збільшенні норми прибутку за безризиковими активами до 25%, ціна ризику (12-25)/21=-0,62, таким чином вона зменшиться. Кут нахилу бюджетної лінії також зменшиться.

13 Вибір рішень в умовах неповної визначеності

Існує ряд альтернативних варіантів модифікації виробу. У табл. 4.19 наведені варіанти модифікації виробу і можливі зна­чення прибутку у випадку реалізації кожного з варіантів. Багатоваріантність прибутків пояснюється невизначеністю оцінки реак­ції споживачів і, отже, обсягів збуту. Використовуючи критерії мінімаксу, максиміну, Севіджа, Гурвіца, оцінити варіанти оформ­лення виробів і вибрати найкращий.

Таблиця 4.19 – Вихідні дані

Варіант модифікації	Можливий результат (прибуток, тис. грн.)				Показник песимізму
А	18	50	22	55	0,3
Б	19	40	35	67
В	-5	25	40	70
Г	15	38	45	64
Д	30	65	35	45

Коли йдеться мова про матрицю прибутків, користуються максимінним критерієм. Згідно з цим критерієм вибирається альтернатива Х^*, яка задовольняє умову

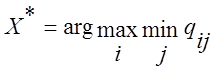                                                 (4.15)

Найменшим прибутком для модифікації виробу А є 18, Б – 19, В – (-5), Г - 15, Д - 30 тис. грн. Найбільшим з них є прибуток для модифікації виробу Д. Тобто найкращий з можливих найгірших результатів гарантує модифікація виробу Д.

Тепер застосуємо критерій Севіджа. Він будується на розрахунку матриці "жалощів", елементи якої S визначаються так:

                                                  (4.16)