Загальні принципи аналізу ризику. Відношення людей до ризику, страница 7

Потрібно визначити оптимальну стратегію поведінки головного економіста. Знайти оптимальне рішення.

Відповідь

Побудуємо "дерево рішень", яке проілюструє проблему і допоможе організувати пошук оптимального рішення (рис.4.3).

А – вихідне становище; Б₁, Б₂, В₁....В₃, Г₁....Г₁₂ – становище або точки розвилки; Д₁....Д₂₁ – кінцеві становища.

Структура задачі наведена на рисунку 4.4

А – вихідне становище; Д₁₀, Д₁₁ – дії першого рівня, Д₂₀, Д₂₁, Д₂₂, Д₂₃ – дії другого рівня; П₁₀, П₁₁, П₁₂ – події першого рівня, П₂₀, П₂₁, П₂₂ – події другого рівня.

На рисунку 4.5 наведено схему попередньої оцінки варіантів дій. Збільшення прибутку позначено знаком „+”, зменшення „-”. В кінцевих точках по кожному з шляхів підраховуються алгебраїчні суми величин зменшення або збільшення 

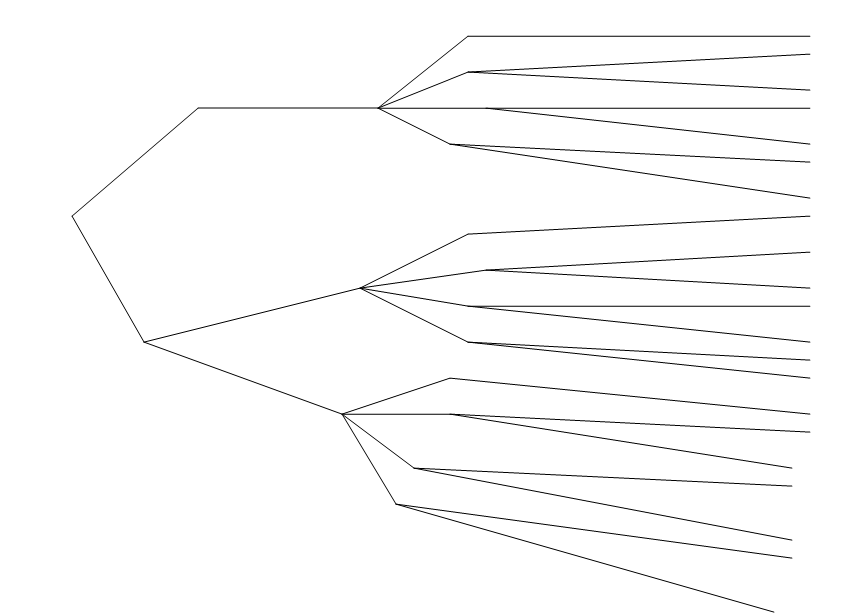
Рисунок 4.4 – Структура задачі

Рисунок 4.5 - Схема попередньої оцінки варіантів дій

Штучним подіям П₁₀, П₂₀ приписуємо імовірність 1,0 Позначимо на "дереві" відомі імовірності подій (рис. 4.6):

Р(П₂₁) = 0,8, Р(П₂₂) = 0,2.

Ймовірність того, що передбачення успіху підтвердиться успішним виведенням нового товару на ринок, становить Р(П₁₁/П₂₁) = 0,88.

Через те, що П₁₁ (подія, що підтверджує успіх) і П₂₁ (подія, що підтверджує невдачу) складають повну систему подій, то ймовірність того, що передбачення успіху не підтвердиться успішним виведенням нового товару на ринок, становить Р(П₁₂/ П₂₁) = 0,12.

Аналогічно ймовірності того, що передбачення невдачі підтвердиться чи не підтвердиться провалом (невдачею) виведення нового товару на ринок відповідно, становлять Р(П₁₂/ П₂₂) = 0,95, Р(П₁₁/ П₂₂) = 0,05.

Розрахуємо апостеріорні ймовірності за формулою Байєса. Ймовірність успіху при передбаченні успіху складає

Р(П₂₁/ П₁₁) = 0,88 · 0,8 / (0,88 · 0,8 + 0,05 · (1 - 0,88)) = 0,991.

Ймовірність невдачі при передбаченні успіху складає

Р(П₂₂/ П₁₁) = 0,05 · 0,2 / (0,05 · 0,2 + 0,88 · (1 - 0,2)) = 0,014.

Ймовірність успіху при передбаченні невдачі складає

Р(П₂₁/ П₁₂) = 0,12 · 0,8 / (0,12 · 0,8 + 0,95 · (1 - 0,8)) = 0,3356.

Ймовірність невдачі при передбаченні невдачі складає

Р(П₂₂/ П₁₂) = 0,95 · 0,2 / (0,95 · 0,2 + 0,12 · (1 - 0,2)) = 0,6643.

Ймовірності передбачення успіху і невдачі відповідно:

Р(П₁₁) = 0,88 · 0,8 / 0,991 = 0,71.

Р(П₁₂) = 0,12 · 0,8 / 0,3356 = 0,29.

Позначимо обчислені ймовірності на рис. 4.6.

           Рисунок 4.6 – Ймовірності

З їх урахуванням для кожного становища (Г₁....Г₁₂) підраховуємо значення очікуваних величин (див. рис. 4.5 і 4.6):

Е(Г₁) = 0;

Е(Г₂) = 7 · 0,8 - 2 · 0,2 = 5,2;

Е(Г₃) = 11 · 0,8 - 6 · 0,2 = 7,6;

Е(Г₄) = 17 · 0,8 - 11 · 0,2 = 11,4;

Е(Г₅) = -0,15;

Е(Г₆) = 6,85 · 0,991 – 2,15 · 0,014 =6,76;

Е(Г₇) = 10,85 · 0,991 – 6,15 · 0,014 =10,67;

Е(Г₈) = 16,85 · 0,991 – 11,15 · 0,014 =16,54;

Е(Г₉) = -0,15;

Е(Г₁₀) = 6,85 · 0,336 – 2,15 · 0,664= 0,874;

Е(Г₁₁) = 10,85 · 0,336 -6,15 · 0,664=1,73;

Е(Г₁₂) =  16,85 · 0,336 – 2,15 · 0,664=2,882

Для кожного становища (В₁, В₂, В₃) вибираємо гілку, до якої належить максимальне очікуване збільшення прибутку. Відповідно очікувані значення будуть: Е(В₁) = 11,4; Е(В₂) = 16,54; Е(В₃) = 4,234. В кожному становищі (Б₁, Б₂) обчислюємо максимальний очікуваний приріст прибутку:

Е(Б₁) = 11,4; Е(Б₂) =  16,54· 0,71 + 4,234 · 0,29 = 12,97.

Знаходячись у вихідному становищі, вибираємо ту гілку, до якої належить максимальний очікуваний результат. У даному випадку варто проводити дослідження, і у разі передбачення успіху розпочинати випуск виробу В-13 (отримаємо дохід у розмірі 16,54 тис. грн..), а у разі передбачення невдачі також розпочинати випуск  виробу В-13 (отримаємо дохід у розмірі 4,234 тис. грн..).

9 Зниження ризику шляхом об'єднання ризи­ків і диверсифікації портфеля інвестицій

Існує декілька варіантів інвестиційних проектів, що відрізня­ються нормою віддачі (табл. 4.15). Необхідно підібрати 2 портфелі інвестицій таким чином, щоб звести ризик до мініму­му. У портфель включати як мінімум 2 проекти. Порівняти варіа­нти і зробити висновки. Обсяг вільних коштів інвестора 550 тис. грн. Ймовірності розвитку подій (підйом, норма, спад) од­накові.