РАБОТА 16. ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ
16.1. Найти и изобразить область определения данной функции:
1)
![]() 2)
2)
![]()
3)![]() 4)
4)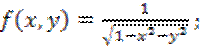
5)![]() 6)
6)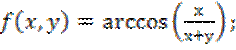
7)![]()
16.2. Для
отображения ![]() найти образ
найти образ ![]() множества
множества ![]() и определить, является ли
и определить, является ли ![]() взаимно однозначным отображением,
если:
взаимно однозначным отображением,
если:
1)
![]()
2)![]()
3)![]()
4)![]()
5)![]()
16.3. Для
отображения ![]() найти образ
найти образ ![]() множества
множества ![]() и определить, является ли
и определить, является ли ![]() взаимно однозначным отображением,
если:
взаимно однозначным отображением,
если:
1)![]()
2)![]()
16.4. Найти
![]() , если
, если ![]() .
.
16.5. Найти
![]() , если
, если 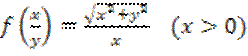 .
.
16.6.
Найти ![]() , если:
, если:
1)![]() 2)
2)![]()
16.7. Пусть
![]() . Найти функцию
. Найти функцию ![]() , если
, если ![]() .
.
16.8. Пусть
![]() . Определить функции
. Определить функции ![]() , если
, если ![]() .
.
16.9. Найти
![]() , если
, если ![]() .
.
16.10. Показать,
что для функции ![]() :
:
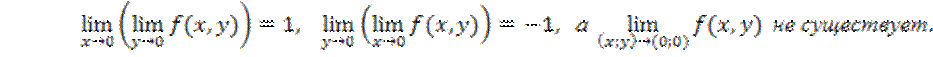
16.11. Показать,
что для функции 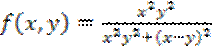 :
:
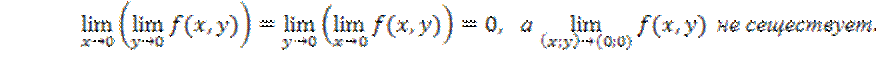
16.12. Показать,
что для функции 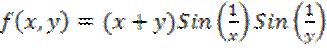 оба повторных предела
оба повторных предела
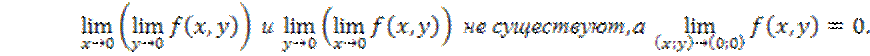
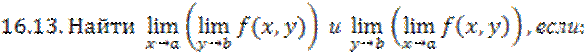
1)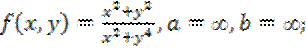 2)
2)![]()
3)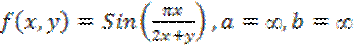 ; 4)
; 4)![]() .
.
16.14. Найти предел:
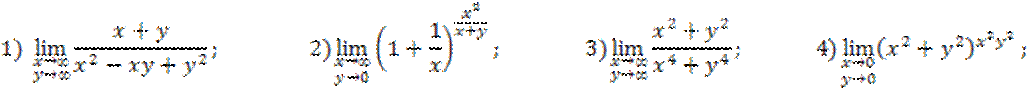
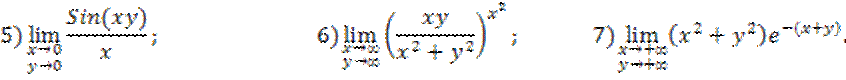
16.15. Будет
ли ![]() фундаментальной
последовательностью в
фундаментальной
последовательностью в ![]() , если:
, если:
1)
![]() 2)
2) ![]() ?
?
16.16. Будет
ли ![]() фундаментальной
последовательностью в
фундаментальной
последовательностью в ![]() , если
, если 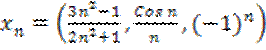 ?
?
16.17. Найти
предел последовательности ![]() в
в ![]() , если
, если 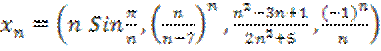 .
.
16.18. Будет ли базой на множестве N следующая системы множеств:
1)
![]() 2)
2) ![]() ;
;
3)
![]() ; 4)
; 4) ![]() ?
?
16.19. Пусть
![]() - последовательность в
- последовательность в ![]() . Что означает существование
предела последовательности по каждой из баз, указанных в задании 16.18? Описать
все сходящиеся по этим базам последовательности.
. Что означает существование
предела последовательности по каждой из баз, указанных в задании 16.18? Описать
все сходящиеся по этим базам последовательности.
16.20. Доказать,
что любое линейное отображение ![]() непрерывно.
непрерывно.
16.21. Пусть
![]() - матрица размеров
- матрица размеров ![]() - фиксированный вектор. Преобразование
- фиксированный вектор. Преобразование
![]() , называется аффинным. Доказать,
что аффинное преобразование непрерывно на
, называется аффинным. Доказать,
что аффинное преобразование непрерывно на ![]() .
.
16.22. Пусть
![]() . Доказать, что отображение
. Доказать, что отображение ![]() непрерывно в точке
непрерывно в точке ![]() тогда и только тогда, когда каждая
координатная функция
тогда и только тогда, когда каждая
координатная функция ![]() непрерывна в точке
непрерывна в точке ![]() .
.
16.23. Доказать,
что отображение ![]() , заданное соотношением
, заданное соотношением 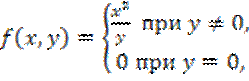 не является непрерывным в точке
(0;0).
не является непрерывным в точке
(0;0).
16.24. Доказать
непрерывность на ![]() отображения
отображения ![]() , если:
, если:
1)
![]() ; 2)
; 2) 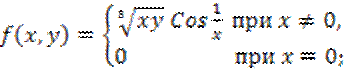
3)
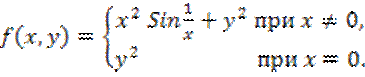
16.25. Пусть
![]() .
.
1)
Показать, что всякая прямая, проходящая через точку (0;0), содержит некоторый
интервал с центром в точке (0;0), принадлежащий множеству ![]() .
.
2)
Пусть отображение ![]() задаётся соотношением
задаётся соотношением 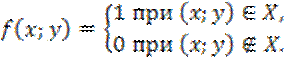 Доказать, что хотя для каждой
точки
Доказать, что хотя для каждой
точки ![]() отображение
отображение ![]() , определённое равенством
, определённое равенством ![]() , непрерывно в 0, сама функция
, непрерывно в 0, сама функция ![]() не является непрерывной в точке
(0;0).
не является непрерывной в точке
(0;0).
16.26. Исследовать
на равномерную непрерывность на ![]() отображение
отображение ![]() , если:
, если:
1)
![]() ; 2)
; 2) ![]() .
.
16.27. Будет
ли равномерно-непрерывным на множестве ![]() отображение
отображение 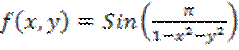 ?
?
16.28. Пусть
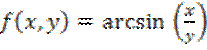 . Является ли отображение
. Является ли отображение ![]() непрерывным в своей области
определения
непрерывным в своей области
определения ![]() ? Будет ли
? Будет ли ![]() равномерно-непрерывным на
равномерно-непрерывным на ![]() ?
?
16.29. Пусть
отображение ![]() задано следующим образом:
задано следующим образом: 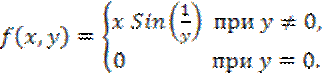
Доказать,
что множество точек разрыва отображения ![]() не является замкнутым.
не является замкнутым.
16.30. Доказать,
что если функция ![]() в некоторой области
в некоторой области ![]() непрерывна по переменной
непрерывна по переменной ![]() и равномерно относительно
и равномерно относительно ![]() непрерывна по переменной
непрерывна по переменной ![]() , то
, то ![]() непрерывна в
непрерывна в ![]() .
.
16.31. Доказать,
что если в некоторой области ![]() функции
функции ![]() непрерывна по переменной
непрерывна по переменной ![]() и удовлетворяет условию Липшица по
переменной
и удовлетворяет условию Липшица по
переменной ![]() , т.е.
, т.е. ![]() , где
, где ![]() - постоянная, то эта функция
непрерывна в
- постоянная, то эта функция
непрерывна в ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.