§ 13. Бесконечно большие последовательности
13.1. Определение бесконечно больших последовательностей.
Определение: Будем говорить, что (xn) д.ч. – бесконечно большая, если "e≥0 $pÎN "nÎN (n ³ p Þ ôxnô³ e), и записывать: lim xn = ∞ или xn → ∞ (читается: xn стремится к бесконечности).
lim xn = ∞ Û " e ≥ 0 $ p Î N " n Î N (n ³ p Þ ôxnô³ e)
Тривиальны следующие три теоремы:
Теорема 1: Для того, чтобы (xn) была бесконечно большой, необходимо и достаточно, чтобы ( |xn| ) стремится к +∞. (lim xn = ∞ Û lim |xn| = -∞).
Геометрически стремление (xn) к ∞ означает, что почти все члены (xn) лежат вне любого конечного отрезка [-e;e].
Теорема 2: Бесконечно большая последовательность неограниченна
(lim xn = ∞ Þ xn ≠ O(1))
<≠ xn ={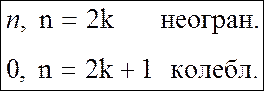
lim |xn| ≠ +∞.
Теорема 3: Если (xn) сходится к ±∞, то она бесконечно большая.
lim ±∞ Þ lim xn = ∞
<≠ xn = (-1)n n.
|
Сходимость в R |
Ограниченно колеблющиеся |
Неограниченно колеблющиеся |
Сходимость к +∞ |
Сходимость к -∞ |
||
|
Бесконечно малые |
Бесконечно большие |
|||||
Ограниченность Неограниченность
13.2 Основные свойства бесконечно больших последовательностей.
Теорема 1:
Если последовательность (yn) бесконечно большая, то lim 
= O.
lim yn = ∞ Þ lim = O.
◄ По условию " e ≥ 0 $ p Î N " n Î N
(n ³ p Þ ôynô³ 
). Тогда " n ≥ p
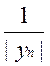≤ e, т.е. lim
= O ►
Теорема 2:
Если (xn) ограниченна, а (yn) –
бесконечно большая, то lim 
= O.
◄ = xn* = т.1 O(1)*o(1) = o(1). Восп. тем, что
ограниченной на бесконечно малую дает
бесконечно малую ►
Теорема 3: Если почти все члены бесконечно малой
последовательности (yn) отличны от нуля, то lim = ∞.
(lim = O и почти все yn отличны
от 0) Þ lim = ∞.
◄" e > 0 $ p Î N
" n Î N (n ³ p Þ ôynô≤ ). Тогда "n ³ p Þ || ³ e).
Это означает, что lim = ∞. ►
Теорему 3 можно рассматривать как обратную к теореме 1.
Теорема 4: если модули почти всех членов (xn) ограниченны снизу положительным числом и почти все
члены бесконечно малой (yn) отличны от 0, то lim = ∞.
(почти все ôxnô³ m
> 0; lim yn = 0, почти yn ≠ 0) Þ lim = ∞.
◄ $ m > 0 $ p1 Î N " n Î N (n ³ p1 Þ ôxnô≥ m)
" e > 0 $ p2 Î N " n Î N
(n ³ p2 Þ ôynô≤ 
)
Тогда " n ³ p = max(p1; p2)
|| = 
≥ 
≥ 
=
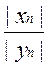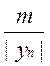e
Т.О. lim || = +∞ Û lim = ∞. ►
Следствие. Если
пост. с ≠ 0, то lim
= 0, при y → ∞;
lim = ∞, при y → O.
13.3 Поведение суммы 2-х последовательностей.
|
(yn) (xn) |
Сходятся в R |
Ограниченно колеблется |
Неограниченно колеблется |
Сходится к +∞ |
Сходится к -∞ |
|
Сходятся в R |
Т.1 |
T.2 |
T.2 |
T.2 |
T.2 |
|
Ограниченно колеблется |
T.2 |
T.6 |
T.7 |
T.3A |
Т.3Б |
|
Неограниченно колеблется |
T.2 |
T.7 |
T.8 |
T.5A |
Т.5Б |
|
Сходится к +∞ |
T.2 |
T.3A |
T.5A |
T.3A |
Т.4 |
|
Сходится к -∞ |
T.2 |
T.3Б |
T.5Б |
T.4 |
Т.3Б |
Т.1 (lim xn = x0 Î R; lim yn = y0 Î R) Þ
lim (xn + yn) = x0 + yn Î R.
T.2 (lim xn = x0 Î R и lim yn = +∞) Þ lim (xn + yn) = +∞
(lim xn = x0 Î R и lim yn = -∞) Þ lim (xn + yn) = -∞
(lim xn = x0 Î R и (yn) огр. колебл) Þ lim (xn + yn) огр. колебл
(lim xn = x0 Î R и (yn) неогр. колебл) Þ lim (xn + yn) неогр. Колебл
◄ Поскольку сходящаяся в R последовательность ограничена, то первые утверждения очевидны из геометрических соображений.
Две последних получены методом от противного yn = (xn + yn) + (-xn)… ►
T.3-А ( lim xn = +∞; lim yn = +∞) Þ lim (xn + yn) = +∞
(lim xn = +∞, (yn) ограниченно колеблется) Þ lim (xn + yn) = +∞
Т.3-Б (lim xn = -∞; lim yn =-∞) Þ lim (xn + yn) =-∞
(lim xn = -∞, (yn) ограниченно колеблется) Þ lim (xn + yn) = -∞
T.4 Если (xn) сходится к +∞, а yn сходится к -∞, то (xn + yn) может либо сходится в R, либо к +∞, либо к -∞,либо ограниченно или неограниченно колеблется.
◄ Все 5 возможностей могут быть проиллюстрированы при
1) xn = n ; yn = -n;
2) xn = n2; yn = -n;
3) xn = n; yn = -n2;
4) xn = n + (-1)n; yn = -n;
5) xn = n2 + (-1)n n; yn = -n2;
►
T.5-A Если (xn) сходится к +∞, а (yn) неограниченно колеблется, то их сумма может сходится к +∞ или неограниченно колебаться, но не может стремится ни к конечному пределу, ни к -∞, ни ограниченно колебаться.
◄ Т.к. yn = (xn + yn) + (-xn), то последние 3 утверждения устанавливаются методом от противного на основании предыдущих теорем.
Примеры двух возможных случаев:
1) xn = n2; yn = (-1)n n;
2) xn = n ; yn = (-1)n n2;
►
T.5Б Если последовательность (xn) сходится к -∞, а (yn) неограниченно колеблется, то их сумма может сходится к -∞ или неограниченно колебаться, но не может сходится ни к конечному пределу, не может стремится к +∞, ни ограниченно колебаться.
Т.6 Если (xn) и (yn) ограниченно колеблются, то их сумма должна либо также ограниченно колебаться, либо сходится к конечному пределу.
◄ Ограниченность (xn + yn) очевидна.
1) xn = (-1)n; yn = (-1)n;
2) xn = (-1)n; yn = (-1)n+1.
►
T.7 Если (xn) колеблется ограниченно, а (yn) – неограниченно, то (xn + yn) колеблется неограниченно.
◄По условию $ m > 0 " n Î N ôxnô≤ m; $ k > 0 $ n Î N ôynô≥ k.
При k>m (xn + yn) ≥ ||xn| - |yn|| = |M-K| > 0 Þ (xn + yn) должна либо сходиться к +∞, либо к -∞, либо неограниченно колебаться.
yn = (xn + yn) + (-xn), поэтому предположение lim (xn + yn) = ±∞ приводит (по т. 3А и 3Б) к противоречию с условием, значит, (xn + yn) неограниченно колеблется.
►
Т.8 Если (xn) и (yn) неограниченно колеблются, то (xn + yn) может либо стремится к конечному пределу, либо к ±∞, либо ограниченно или неограниченно колеблется.
◄Примеры:
1) xn = (-1)n n; yn = (-1)n+1 n;
2) xn = (-1)n n; yn = (1 + (-1)n+1) n;
3) xn = (-1)n n; yn = (-1 + (-1)n+1) n;
4) xn = (-1)n n; yn = (-1)n+1 (n+1);
5) xn = (-1)n n; yn = (-1)n n;
►
Если мы захотим выяснить поведение произведения (xn + yn), то в случае сходимости в R надо различать lim xn = 0 и lim xn = x0 ≠ 0.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
