Контрольная работа по теме
" Дифференциальное исчисление и экстремумы функций нескольких переменных "
I вариант
1
Определение частного приращения функции в точке по переменной ![]() .
.
2
Найти и изобразить область определения функции ![]() .
.
3 Найти
частные производные и дифференциал функции ![]() .
.
4 Найти ![]() , если
, если ![]() ,
, ![]() .
.
5 Найти
дифференциал второго порядка ![]() функции
функции ![]() .
.
6Найти частные
производные неявно заданной функции ![]()
![]() .
.
7 Найти производные функции ![]() по направлению
по направлению
![]() в
точке
в
точке ![]() .
.
8 Исследовать
на экстремум функцию ![]()
9 Найти
наибольшее и наименьшее значения функции ![]() в области
в области
![]() ,
,
ограниченной
линиями ![]() ;
;
![]() .
.
II вариант
1 Определение сложной функции многих переменных
2 Найти
и изобразить область определения функции ![]() .
.
3
Найти частные производные и дифференциал функции ![]() .
.
4 Найти 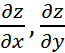 , если
, если ![]() .
.
5
Найти дифференциал второго порядка ![]() функции
функции ![]() .
.
6 Найти частные производные неявно заданной функции :
![]() .
.
7
Найти градиент функции ![]() в точке
в точке ![]() .
.
8 Исследовать
на экстремум функцию ![]() .
.
9
Найти наибольшее и наименьшее значения функции z=z(x,y)
в области ![]() ,
,
ограниченной линиями ![]()
III вариант
1 Определение градиента функции в точке.
2
Найти и изобразить область определения функции ![]() .
.
3
Найти частные производные и дифференциал функции ![]() .
.
4
Найти ![]() , если
, если ![]() .
.
5
Найти дифференциал второго порядка ![]() функции
функции ![]() .
.
6 Найти
частные производные неявно заданной функции ![]()
![]() .
.
7 Найти производные функции по направлению биссектрисы первой четверти
в точке ![]() функции
функции 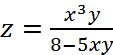 .
.
8
Исследовать на экстремум функцию ![]() .
.
9 Найти наибольшее и наименьшее значения функции z=z(x,y) в области
![]() , ограниченной линиями
, ограниченной линиями ![]() .
.
IV вариант
1 Определение полного приращения функции нескольких переменных в точке.
2
Найти и изобразить область определения функции ![]() .
.
3
Найти частные производные и дифференциал функции ![]() .
.
4
Найти ![]() , если
, если ![]() .
.
5
Найти дифференциал второго порядка ![]() функции
функции ![]() .
.
6
Найти частные производные неявно заданной функции ![]()
![]() .
.
7
Найти градиент функции в точке ![]() в точке
в точке ![]() .
.
8
Исследовать на экстремум функцию ![]() .
.
9
Найти наибольшее и наименьшее значения функции ![]() в области
в области
![]() , ограниченной линиями
, ограниченной линиями ![]() .
.
V вариант
1
Определение частной производной функции нескольких переменных по переменной ![]() в точке.
в точке.
2
Найти и изобразить область определения функции ![]() .
.
3
Найти частные производные и дифференциал функции ![]() .
.
4
Найти 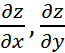 , если
, если ![]() .
.
5
Найти дифференциал второго порядка ![]() функции
функции ![]() .
.
6
Найти частные производные неявно заданной функции ![]()
![]() .
.
7
Найти производные функции в точке ![]()
![]() .
.
8
Исследовать на экстремум функцию ![]() .
.
9
Найти наибольшее и наименьшее значения функции ![]() в области
в области ![]() ,
,
ограниченной
линиями ![]() .
.
VI вариант
1 Определение производной функции по направлению в точке.
2 Найти и
изобразить область определения функции ![]() .
.
3 Найти
частные производные и дифференциал функции ![]() .
.
4 Найти ![]() , если
, если ![]() .
.
5 Найти
дифференциал второго порядка ![]() функции
функции ![]() .
.
6Найти частные
производные неявно заданной функции ![]()
![]() .
.
7 Найти
градиент функции ![]() в точке
в точке ![]() .
.
8 Исследовать
на экстремум функцию ![]() -
-![]() .
.
9 Найти
наибольшее и наименьшее значения функции ![]() в области
в области
![]() ,ограниченной линиями
,ограниченной линиями ![]() .
.
Контрольная работа по теме
" Криволинейные и двойные интегралы "
I вариант
1 Вычислить
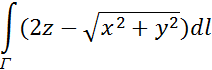
где Г - кривая, заданная параметрическими уравнениями ![]() .
.
2
Вычислить
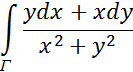
где Г - отрезок прямой ![]() .
.
3
Вычислить
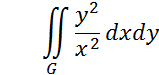
где G - область, ограниченная линиями ![]() .
.
4 Вычислить
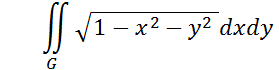
Где D – область , заданная уравнением ![]() .
.
5
Представить двойной интеграл
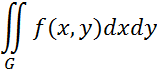
в виде повторного интеграла с внешним интегрированием по x и
внешним интегрированием по y, если область G задана линиями
![]() ,
, ![]() .
.
II вариант
1 Вычислить
массу дуги кривой ![]() с плотностью
с плотностью ![]() , если концы дуги определены значениями x:
, если концы дуги определены значениями x:
![]() ,
, ![]() .
.
2 Вычислить
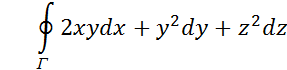
Где Г- дуга линии ![]() ,
, ![]() ,
, ![]() от точки
от точки ![]() до точки
до точки ![]() .
.
3
Вычислить
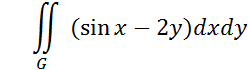
где G- область ограниченная линиями ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
4
Вычислить
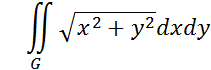
Где
область G есть ![]() ,
, ![]() .
.
5 Представить двойной интеграл
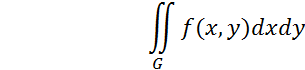 в виде повторного интеграла с внешним интегрированием по x и
в виде повторного интеграла с внешним интегрированием по x и
внешним
интегрированием по y, если область G задана линиями
![]() ,
, ![]() .
.
III вариант
1
Вычислить
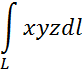
Где ![]() - отрезок
прямой
- отрезок
прямой ![]() .
.
2
Найти работу силы ![]() вдоль кривой
вдоль кривой ![]() =1 от точки
=1 от точки ![]() до точки
до точки
![]() .
.
3
Вычислить
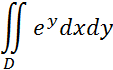
Где область ![]() ограничена
линиями
ограничена
линиями ![]() ,
,![]() ,
,![]() .
.
4
Вычислить
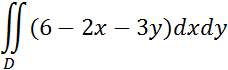
Где D – область , задана уравнением ![]()
5 Представить двойной интеграл
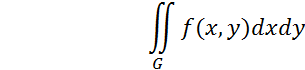 в виде повторного интеграла с внешним интегрированием по x и
в виде повторного интеграла с внешним интегрированием по x и
внешним
интегрированием по y, если область G задана линиями
![]() ,
, ![]() .
.
IV вариант
1
Найти массу линии ![]() между точками
между точками ![]() , для которых ординаты равны 0 и
, для которых ординаты равны 0 и ![]() , если в каждой точке линии
, если в каждой точке линии ![]() плотность
плотность
пропорциональна квадрату абсциссы точки.
2
Найти работу силы ![]() вдоль пути
вдоль пути ![]() ,
,![]() ,
, ![]() ,
, ![]() .
.
3
Вычислить
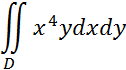
Где область ![]() ограничена
линиями
ограничена
линиями ![]() ,
, ![]() ,
, ![]() .
.
4
Вычислить
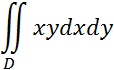
Где область ![]() ограничена
линиями
ограничена
линиями ![]() ,
, ![]() ,
,![]() .
.
5 Представить двойной интеграл
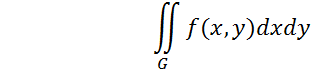 в виде повторного интеграла с внешним интегрированием по x и
в виде повторного интеграла с внешним интегрированием по x и
внешним интегрированием по y, если область G задана линиями
![]() ,
, ![]() ,
,![]() ,
,![]() .
.
V вариант
1
Найти длину дуги кривой ![]() от точки
от точки ![]() до точки
до точки ![]() .
.
2
Вычислить
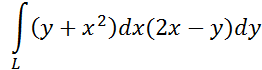
где – дуга кривой ![]() , расположенной между точками
, расположенной между точками![]() .
.
3 Вычислить
площадь фигуры , ограниченной линиями ![]() ,
, ![]() .
.
4
Вычислить
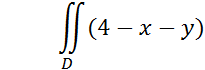
Где D – область , заданная уравнением ![]() .
.
5 Представить двойной интеграл
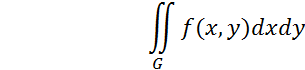 в виде повторного интеграла с внешним интегрированием по x и
в виде повторного интеграла с внешним интегрированием по x и
внешним интегрированием по y, если область G задана линиями
![]() ,
,![]() ,
,![]() ,
,![]() .
.
VI вариант
1 Вычислить
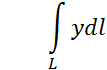
где L- дуга параболы ![]() , отсеченная параболой
, отсеченная параболой ![]() .
.
2 Найти работу силы ![]() при перемещении точки по дуге кривой
при перемещении точки по дуге кривой ![]() .
.
3
Найти массу пластинки ![]() ,
,![]() , если
, если ![]() .
.
4
Вычислить
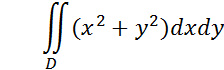
Где D – область , задана уравнением ![]() .
.
5 Представить двойной интеграл
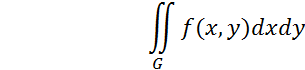 в виде повторного интеграла с внешним интегрированием по x и
в виде повторного интеграла с внешним интегрированием по x и
внешним интегрированием по y, если область G задана линиями
![]() ,
,![]() ,
,![]() ,
,![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.