§ 18. Бесконечно малые и бесконечно большие функции.
18.1. Бесконечно малые функции.
Определение 1. Функция f(x) называется бесконечно малой функцией (или просто бесконечно малой) в точке x = x0 (или при x ®x0), если lim f(x) = 0.
x ® x0
Аналогично бесконечно малые определяются при x ® ¥, при x ® –¥, при x ® +¥; x ® x0+, x ® x0-.
На «языке e - d»:
f(x) – бесконечно малая при x ® x0, если "e > 0 $ d > 0 "x Î x (0 < |x – x0| < d Þ |f(x)| < e)
На языке последовательностей:
f(x) – бесконечно малая при x ®x0, если "(xn), xn ® x0 последовательности (f(xn)) является бесконечно малой последовательностью, то есть lim f(xn) = 0.
n® ¥
Теорема 18.1 Для выполнения равенства lim f(x) = A необходимо и достаточно, чтобы
x ® x0
функция j(x) = f(x) – A была бесконечно малой при x ® x0.
![]() Доказывается просто
Доказывается просто ![]()
Говорят, что f(x) в окрестности точки x = x0 отлична от своего предела A на бесконечно малую функцию.
Бесконечно малые функции, как и бесконечно малые последовательности, обладают следующими свойствами:
18.2. Бесконечно большие функции.
Определение 2. f(x) – бесконечно большая функция (или просто бесконечно большая) в точке x = x0 (или при x ® x0), если " e > 0 $ d > 0 такое, что "x Î x, x ¹ x0, удовлетворяющих неравенству |x –x0| < d, выполняется неравенство |f(x)| > e. Пишут: lim f(x) = ¥.
x ® x0
Если же выполняется неравенство f(x) > e (f(x) < –e), пишут lim f(x) = +¥ (lim = –¥).
x ® x0 x ® x0
Говорят, что f(x) имеет в точке x0 бесконечный предел, равный +¥ (–¥). Аналогично определяется односторонние пределы и пределы при x ® ¥ (x ® +¥, x ® –¥).
Оказывается, что функция, обратная бесконечно малой, является бесконечно большой и наоборот. (Доказать самостоятельно)
18.3. Сравнение бесконечно малых и бесконечно больших функций.
Сумма, разность, произведение бесконечно малых функций есть функции бесконечно малые. А о частном бесконечно малых заранее ничего определенного сказать нельзя:
![]()
![]() 1. a(x) = x; b(x) = 2x. lim
1. a(x) = x; b(x) = 2x. lim 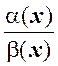 = lim
= lim ![]() =
=![]() .
.
2. a(x) = x; b(x) = x2.
![]()
![]()
![]()
![]() lim
lim 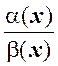 = lim
= lim ![]() = lim
= lim ![]() = ¥. lim
= ¥. lim 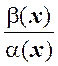 = 0.
= 0.
Правила сравнения бесконечно малых функций:
Пусть при x ® x0 функции a(x) и b(x) являются бесконечно малыми, тогда:
![]() 1. Если lim
1. Если lim 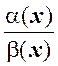 = 0, то a(x) –
бесконечно малая более высокого порядка, чем b(x):
= 0, то a(x) –
бесконечно малая более высокого порядка, чем b(x):
a(x) = o(b(x)).
![]() 2. Если lim
2. Если lim 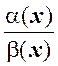 = A ¹ 0, то a
и b – бесконечно малые одного порядка:
= A ¹ 0, то a
и b – бесконечно малые одного порядка:
a(x) = O(b(x)).
![]() 3. Если lim
3. Если lim 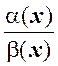 = 1, то a и b – эквивалентные
бесконечно малые a ~ b.
= 1, то a и b – эквивалентные
бесконечно малые a ~ b.
![]() 4. Если lim
4. Если lim 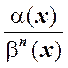 = A ¹ 0, то a(x) – бесконечно малая n-ого порядка относительно b(x).
= A ¹ 0, то a(x) – бесконечно малая n-ого порядка относительно b(x).
Аналогичные определения вводятся и в случае односторонних пределов при x ® ¥, x ® +¥, x ® –¥.
q
![]() 1) sin x ~ x при x ® 0, так как
lim
1) sin x ~ x при x ® 0, так как
lim 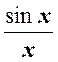 = 1.
= 1.
2) sin 3x и sin 2x – бесконечно малые одного порядка при x ® 0:
![]()
![]()
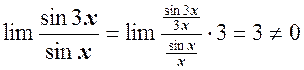 .
.
3) a(x) = 1 – cos x Þ a(x) = O(x2).
![]() a(x) = 1 – cos x = 2sin2
a(x) = 1 – cos x = 2sin2![]() Þ lim
Þ lim 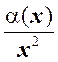 = lim
= lim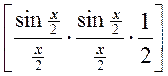 =
= ![]() ¹ 0.
¹ 0. ![]()
![]()
![]()
![]()
![]() Теорема 18.3 Пусть a(x), a1(x),
b(x)
и b1(x)
– бесконечно малые функции при x ® x0, причем a(x) ~ a1(x) при x ® x0, b(x) ~ b1(x) при x ® x0 и $
lim
Теорема 18.3 Пусть a(x), a1(x),
b(x)
и b1(x)
– бесконечно малые функции при x ® x0, причем a(x) ~ a1(x) при x ® x0, b(x) ~ b1(x) при x ® x0 и $
lim 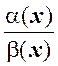 . Тогда $ lim
. Тогда $ lim 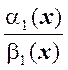 и
и 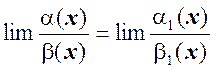 .
.
![]()
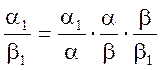
![]()
q
![]() Найти lim
Найти lim 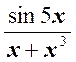 .
.
![]()
![]() Решение. Так как sin 5x ~ 5x, а x
+x3
~x при
x ® 0, то
Решение. Так как sin 5x ~ 5x, а x
+x3
~x при
x ® 0, то 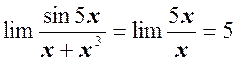 .
.
Для бесконечно больших функций имеются аналогичные правила сравнения.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.