Функции комплексной переменной. Множества, кривые, области. Предел последовательности

Тема 1 Функции комплексной переменной

Практическое занятие 1 Функции комплексной переменной

1.1 Множества, кривые, области

1.2 Предел последовательности

1.3 Предел и непрерывность функции комплексной переменной

1.4 Основные элементарные функции комплексной переменной

1.1 Множества, кривые, области

Множество точек плоскости , удовлетворяющих неравенству , называется ε-окрестностью точки :

.

Множество точек комплексной плоскости, удовлетворяющих условию , называется - окрестностью бесконечно удаленной точки :

.

Комплексная плоскость вместе с бесконечно удаленной точкой  называется расширенной комплексной плоскостью. Символы , ,  задают направления на плоскости .

Точка  называется предельной точкой множества , если в любой окрестности точки  расположено бесконечно много точек . Предельная точка  может принадлежать множеству , а может и не принадлежать ему.

Точка  называется внутренней точкой множества , если существует такое , что окрестность  состоит только из точек множества . Множество называется открытым, если каждая точка этого множества является его внутренней точкой.

Точка  расширенной комплексной плоскости называется граничной точкой множества , если при любом  окрестность  содержит точки  и точки . Граничная точка множества  может принадлежать множеству , а может и не принадлежать ему. Совокупность всех граничных точек множества называется границей множества. Множество , содержащее свою границу, называется замкнутым и обозначается .

Пусть . Если каждому значению  поставлено в соответствие , то говорят, что на множестве  задана комплекснозначная функция действительной переменной : .

Полагая , можно считать, что задание функции  равносильно заданию на множестве  двух действительных функций  и  переменной . Очевидно, если  и  непрерывные функции, то и функция  является непрерывной. Графиком функции  является кривая на комплексной плоскости . Точкой самопересечения кривой  называется точка , для которой при  имеет место соотношение .

Кривой Жордана называется непрерывная кривая , , не имеющая точек самопересечения. Замкнутой кривой называется кривая Жордана, у которой конец совпадает с началом (совпадение начала и конца замкнутой кривой не считается точкой самопересечения). Кривая Жордана  называется гладкой, если функции  и  непрерывно-дифференцируемы и  на множестве . Кривая Жордана называется кусочно-гладкой, если она состоит из конечного числа гладких кривых.

Множество  называется связным множеством, если две любые его точки можно соединить кривой Жордана, целиком лежащей в . Связное открытое множество  называется областью.

а)	б)
Рисунок 1. 1 – Односвязная (а) и многосвязная (б) области

Область, ограниченная замкнутым контуром , обозначается . Область  называется односвязной, если любой замкнутый контур  целиком лежащий в , ограничивает область  (рисунок 1. 1, а). В противном случае область называется многосвязной (рисунок 1. 1, б).

Для многосвязной области  найдутся контуры , , …, , такие, что точки из областей , , …,  не входят в . С помощью дополнительных разрезов , , ...,  многосвязная область преобразуется в односвязную (рисунок 1. 2), так как в области с разрезами любой замкнутый контур  не будет содержать внутри себя точек из областей , , …, .

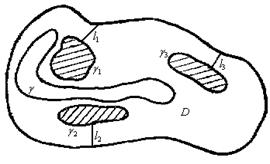
Рисунок 1. 2 – Многосвязная область  и ее разрезы , ,

Положительным направлением обхода границы области  считается то направление, при котором область  остается слева.

1.2 Предел последовательности

Пусть дана последовательность комплексных чисел

, ... .

Число ,  называется пределом числовой последовательности , если для любого  существует номер  такой, что для всякого  справедливо неравенство :

  .

Комплексное число  называется пределом последовательности , если  найдется такой номер , что для любого  выполняется неравенство :

  .

Теорема 1 Для того чтобы существовал конечный предел  последовательности , , необходимо и достаточно, чтобы существовали пределы последовательностей действительных чисел  и  и , .

Пусть  и  показательные формы для  и  соответственно.

Теорема 2 Для того чтобы существовал конечный предел , , последовательности , необходимо и достаточно, чтобы существовал предел , а при соответствующем выборе области главных значений аргументов  и  существовал предел .

Последовательность  называется ограниченной, если существует число  такое, что все элементы последовательности удовлетворяют неравенству .

Сходящиеся последовательности комплексных чисел обладают свойствами:

– сходящаяся последовательность имеет только один предел;

– сходящаяся последовательность ограничена;

– если последовательность  сходится, то она ограничена:

   ;

– сумма (разность) двух сходящихся последовательностей есть сходящаяся последовательность, предел которой равен сумме пределов последовательностей:

;

– произведение  двух сходящихся последовательностей есть сходящаяся последовательность предел которой равен произведению пределов последовательностей:

;

– частное двух сходящихся последовательностей  и , , есть сходящаяся последовательность предел которой равен частному пределов последовательностей: