Теория Бора для водородоподобных атомных систем

ТЕОРИЯ БОРА ДЛЯ ВОДОРОДОПОДОБНЫХ АТОМНЫХ СИСТЕМ

            Цель занятия: Научиться решать задачи с применением основных положений теории Бора для водородоподобных атомных систем.

            Водородоподобная атомная система состоит из положительно заряженного ядра и одного электрона, движущегося вокруг ядра по замкнутой траектории (орбите). Теория Бора базируется на законах классической механики и квантовых постулатах Бора, согласно которым:

1.  Атомы и атомные системы могут длительное время, не излучая и не поглощая энергии, находиться в стационарных состояниях, которым соответствуют значения энергии , образующие дискретный ряд.

2.  Переходя из стационарного состояния с энергией  в состояние с энергией , атом излучает или поглощает квант электромагнитного излучения, частота которого определяется правилом частот Бора

,

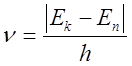где   - постоянная Планка.

3.  Электрон может находиться только на таких орбитах, при движении по которым он имеет момент количества движения, кратный приведенной постоянной Планка :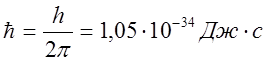

,  

где  - масса электрона,  - его скорость,  - радиус -й орбиты.

            Энергия электрона, находящегося в -м стационарном состоянии, определяется формулой

,

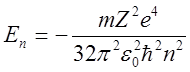где Z – порядковый номер химического элемента в Периодической системе                    Д.И. Менделеева,  Ф/м – диэлектрическая постоянная.

            Спектральные линии, соответствующие квантовым переходам с излучением или поглощением энергии, могут быть объединены в спектральные серии. При этом длина волны электромагнитного излучения, испускаемого или поглощаемого атомом, определяется по обобщенной формуле Бальмера:

,

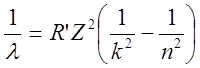где   м^-1 – постоянная Ридберга. Квантовой число  определяет спектральную серию. Переходам из возбужденных состояний атома в основное (нормальное) состояние, для которого , соответствуют спектральные линии, объединенные в серию Лаймана. При  и  регистрируется серия Бальмера. Значениям  и  отвечает серия Пашена,  и  - серия Брэкета,  и  - серия Пфунда,  и  - серия Хэмфри и т.д.

            Частоту излучения можно выразить через волновое число 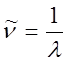 по формуле , где  - скорость света в вакууме. Тогда обобщенную формулу Бальмера можно записать в виде:

,

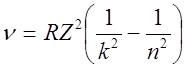где  с^-1.

1. Задачи для коллективного  анализа и самостоятельного решения

1.1.  Основываясь на модели атома, предложенной Бором, получите формулы, определяющие радиус -й орбиты и скорость движения электрона в этом состоянии в водородоподобном атоме. Постройте графики зависимости скорости электрона и радиуса его орбиты от номера квантового состояния.

1.2.  Выведите формулы для потенциальной, кинетической и полной энергии электрона, движущегося по -й орбите в водородоподобном атоме.

1.3.  Вычислите радиусы первой и  второй боровских орбит для электрона, движущегося в атоме водорода и ионах , . Сравните результаты. Постройте график зависимости .

1.4.  Определите частоту  вращения электрона по второй боровской орбите атома водорода.                                                                                          (Ответ:  с^-1)

1.5.  Определите кинетическую, потенциальную и полную энергию электрона, движущегося по первой боровской орбите в атоме водорода и ионах , . Сравните результаты.

1.6.  Вычислите наибольшую и наименьшую длины волн спектральных линий водорода: а) в видимой области спектра; б) в ультрафиолетовой области спектра; в серии Пашена.  

(Ответы  м,  м;  м,  м;  м,  м)

            1.7. Определите: а) потенциал ионизации атома водорода; б) первый потенциал возбуждения атома водорода; в) энергию ионизации атома водорода из первого возбужденного состояния.                                       (Ответы: 13,6 В; 10,2 В;  )

            1.8. Какой серии принадлежит спектральная линия атомарного водорода, волновое число которой равно разности волновых чисел следующих двух линий: 486,1 нм; 410,2 нм? Какова длина волны этой линии?                                          (Ответ: м)

2. Задачи для самостоятельного решения

            2.1. Вычислите энергию фотона, испускаемого при переходе электрона в атоме водорода с третьего энергетического уровня на первый.                            (Ответ: 12,1 эВ)

            2.2. Определите наибольшую и наименьшую энергии фотонов в серии Лаймана атома водорода.                                                                               (Ответы: 10,2 эВ; 13,6 эВ)