Уровни энергии и спектры атомов щелочных металлов. Квантово-механическое описание атомов с эквивалентными электронами. Применение теории возмущений для определения энергии системы тождественных частиц

Лекция 14

Уровни энергии и спектры атомов щелочных металлов

1 Модель валентного электрона.

2 Квантовый дефект и снятие вырождения по орбитальному квантовому числу.

3 Спектральные серии атомов щелочных металлов

4 Дублетная структура спектральных линий как следствие спин-орбитального взаимодействия.

.

Квантовомеханический расчет сложных атомов, в состав которых входит несколько электронов, движущихся в поле ядра, является сложной математической задачей. Однако для атомов щелочных металлов (, , , , , ), располагающихся в первой группе Периодической системы элементов Д.И. Менделеева, задача может быть упрощена, а их спектральные свойства могут быть легко объяснены на основе расчета, аналогичного проведенному при решении задачи о водородоподобном атоме. Возможность отмеченного упрощения может быть обоснована следующим образом.

Электронные конфигурации атомов щелочных металлов в основном состоянии таковы:

   ;

  ;

  

и т.д. Общей закономерностью их электронного строения является то, что совокупность  электронов полностью заполняет внутренние оболочки атома, (это соответствует электронной конфигурации атома инертного газа из предыдущего периода системы Д.И. Менделеева), а один электрон (валентный) расположен во внешней -оболочке. Известно, что атомы инертных газов характеризуются высокой устойчивостью, тогда как атомы щелочных металлов легко ионизируются. Таким образом, электроны внутренних оболочек с общим отрицательным зарядом  вместе с ядром, положительный заряд которого , образуют устойчивый «остов» атома с суммарным зарядом . В поле этого остова, называемого также эффективным ядром, движется валентный (оптический) -электрон.

Следовательно, электронное строение атома щелочного металла имеет аналогию со строением водородоподобного атома, что и позволяет воспользоваться методикой решения квантовомеханической задачи об атоме водорода (смотри лекцию 10). Однако при этом следует обратить внимание и на существенное отличие атома щелочного металла от атома водорода. В атоме водорода единственный электрон, состояние которого полностью определяет состояние атома, движется в поле, создаваемом ядром. Поскольку линейные размеры ядра (~10^-15 м) во много раз меньше расстояния между электроном и ядром (~10^-10 м), то заряд ядра можно считать точечным, а создаваемое им поле – кулоновским (потенциальная энергия электрона ). В атоме щелочного металла поле создается остовом, линейные размеры которого сравнимы с расстоянием от валентного электрона до ядра.

Рассматривая остов как сложную объемную систему с суммарным зарядом , потенциальную энергию валентного электрона в поле эффективного ядра можно представить в виде ряда

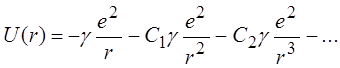 ,              (14.1)

первый член которого учитывает кулоновское взаимодействие электронов с ядром; сохранение в (14.1) двух первых членов соответствует так называемому дипольному приближению, трех первых членов – квадрупольному приближению.

Ограничиваясь в первом приближении двумя первыми членами разложения (14.1) и преобразуя уравнение Шредингера аналогично тому, как это было сделано для атома водорода, получим для угловой функции уравнение, полностью совпадающее с (10.4), а уравнение для радиальной функции  запишем в виде

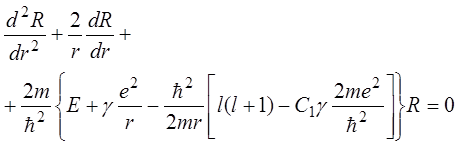       (14.2)

Сравнивая (10.13) и (14.2), видим, что выражение для потенциальной энергии  содержит дополнительный член 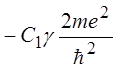 , появившийся в результате учета второго слагаемого в уравнении (14.1). Уравнения (10.13) и (14.2) формально тождественны, если положить в (14.2)

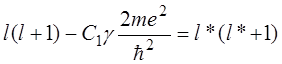.                     (14.3)

Разрешив уравнение (14.3) относительно , получим:

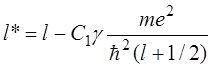.                               (14.4)

Решение уравнения (14.2) с учетом (14.3) приводит к следующему выражению для собственных значений оператора Гамильтона:

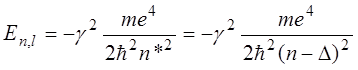.               (14.5)

Эффективное квантовое число  отличается от главного квантового числа  на величину квантового дефекта , обусловленного отличием  от  (смотри формулу (14.4)). Действительно,

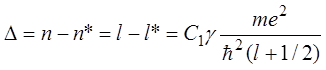,           (14.6)

поэтому энергия электрона в атоме щелочного металла отличается от энергии электрона, находящегося на - уровне в атоме водорода.

Существенно, что наименьшее из значений  всегда больше единицы; например, для  =1,63, для  =1,80 и т.д. Поэтому потенциалы ионизации и резонансные потенциалы щелочных металлов значительно меньше, чем у водорода.

Заметим, что квантовый дефект  определяется орбитальным квантовым числом . Это означает, что в атоме щелочного металла энергия валентного электрона зависит не только от главного квантового числа , но и от орбитального квантового числа , на что в выражении (14.5) указывает индекс . Таким образом, наличие квантового дефекта приводит к снятию вырождения энергетических уровней электрона по орбитальному квантовому числу . Поскольку при заданном  орбитальное квантовое число принимает  различных значений ( 1, 2, …, ), то степень вырождения по  любого -уровня равна , то есть уровень  для атома щелочного металла расщепляется на  компонент .

Воспользуемся формулами (14.5) и (14.6) и в качестве примера рассмотрим схему энергетических уровней атома лития.