ФУНКЦИЯ СОСТОЯНИЯ. РАСЧЕТ ВЕРОЯТНОСТЕЙ
СОСТОЯНИЙ МИКРОЧАСТИЦЫ
Вероятность
нахождения частицы в объеме ![]()
![]() ,
,
где ![]() -
функция состояния (волновая функция) частицы,
-
функция состояния (волновая функция) частицы, ![]() - функция,
комплексно сопряженная с
- функция,
комплексно сопряженная с ![]() ;
; ![]() - квадрат модуля функции состояния,
характеризующий плотность вероятности обнаружения частицы в состоянии, которому
отвечает функция
- квадрат модуля функции состояния,
характеризующий плотность вероятности обнаружения частицы в состоянии, которому
отвечает функция ![]() .
.
Для стационарных состояний
![]() ,
,
где ![]() -
координатная (амплитудная) часть волновой функции.
-
координатная (амплитудная) часть волновой функции.
Условие нормировки вероятностей
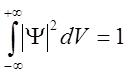 ,
,
где интегрирование производится
по всему бесконечному пространству, то есть по координатам x,
y, z от ![]() до
до ![]() ,
, ![]() .
.
При использовании
сферических координат![]() ;
; ![]() , и
переменные изменяются в диапазонах
, и
переменные изменяются в диапазонах ![]() ;
; ![]() ;
; ![]() .
.
Вероятность
обнаружения частицы в интервале от ![]() до
до ![]()
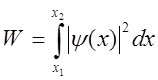 .
.
Среднее значение
физической величины A, характеризующей частицу,
находящуюся в состоянии, которому соответствует волновая функция ![]() ,
,
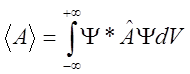 ,
,
где ![]() -
соответствующий оператор,
-
соответствующий оператор, ![]() - нормированная функция
состояния,
- нормированная функция
состояния, ![]() - элемент объема.
- элемент объема.
Основные квантовомеханические операторы:
проекция и квадрат
импульса ……….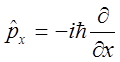 ;
; ![]() ;
;
полная энергия
(гамильтониан) ……..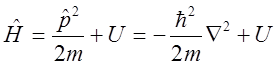 ;
;
проекции момента
импульса ………..![]() ;
; ![]() ;
;
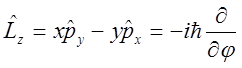 ;
;
квадрат момента
импульса …………..![]() .
.
Здесь ![]() -
оператор Лапласа; его вид в сферических координатах:
-
оператор Лапласа; его вид в сферических координатах:
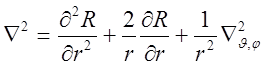 ;
;
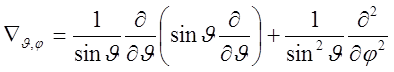 ,
,
где ![]() -
угловая часть оператора Лапласа.
-
угловая часть оператора Лапласа.
Собственные значения
и собственные функции оператора ![]() :
:
![]() ,
, ![]() 0, 1, 2,
….
0, 1, 2,
….
![]() ,
, ![]() .
.
Функции ![]() для
s-, p- и d- состояний приведены в таблице 1 (с точностью до
нормировочного множителя).
для
s-, p- и d- состояний приведены в таблице 1 (с точностью до
нормировочного множителя).
Таблица 1
|
Состояние |
|
|
|
s |
0, 0 |
1 |
|
p |
1, 0 1, 1 |
|
|
d |
2, 0 2, 1 2, 2 |
|
Функции ![]() ,
где
,
где ![]() ,
, ![]() -
первый боровский радиус, приведены в таблице 2.
-
первый боровский радиус, приведены в таблице 2.
Таблица 2
|
Состояние |
|
|
|
|
1, 0 |
|
|
|
2, 0 |
|
|
|
2, 1 |
|
|
|
3, 0 |
|
|
|
3, 1 |
|
|
|
3, 2 |
|
Для электрона, входящего в состав атома водорода:
· орбитальные моменты импульса и магнитный момент электрона:
![]() ;
; ![]() ,
,
где ![]() -
орбитальное квантовое число, которое может принимать значения 0, 1, 2, …,
-
орбитальное квантовое число, которое может принимать значения 0, 1, 2, …, ![]() ;
; ![]() -
магнетон Бора (
-
магнетон Бора (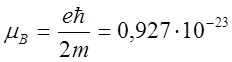 Дж/Тл);
Дж/Тл);
· проекция орбитальных момента импульса и магнитного момента на направление внешнего магнитного поля (совпадающего с осью Z):
![]() ;
; ![]() ,
,
где ![]() -
магнитное квантовое число;
-
магнитное квантовое число;
· гиромагнитное отношение для орбитальных магнитного и механического моментов
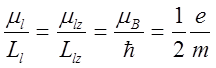 ;
;
· спиновые момент импульса и магнитный момент электрона
![]() ;
; ![]() ,
,
где ![]() -
спиновое квантовое число (для электрона
-
спиновое квантовое число (для электрона ![]() );
);
· проекции спиновых момента импульса и магнитного момента на направление внешнего магнитного поля (совпадающего по направлению с осью Z)
![]() ;
; ![]() ,
,
где ![]() -
спиновое магнитное квантовое число (
-
спиновое магнитное квантовое число (![]() ; +1/2);
; +1/2);
· гиромагнитное отношение для спиновых магнитного и механического моментов
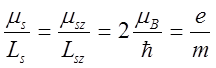 .
.
1.
Функция состояния некоторой частицы может быть представлена в виде ![]() . Покажите, что плотность вероятности
нахождения частицы определяется только координатной частью функции состояния
. Покажите, что плотность вероятности
нахождения частицы определяется только координатной частью функции состояния ![]() .
.
2.
Функция состояния некоторой частицы имеет вид 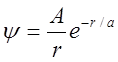 ,
где
,
где ![]() - расстояние этой частицы до силового
центра;
- расстояние этой частицы до силового
центра; ![]() - некоторая постоянная. Используя условие
нормировки вероятностей, определите нормирующий множитель
- некоторая постоянная. Используя условие
нормировки вероятностей, определите нормирующий множитель ![]() .
.
Ответ: ![]()
3.
Используя условие нормировки вероятностей, определите нормирующий
множитель волновой функции ![]() , описывающей основное
состояние электрона в атоме водорода, где
, описывающей основное
состояние электрона в атоме водорода, где ![]() -
расстояние электрона от ядра,
-
расстояние электрона от ядра, ![]() - первый боровский
радиус.
- первый боровский
радиус.
Ответ:
![]()
4. Волновая
функция ![]() определена только в области
определена только в области ![]() . Используя это условие, определите
нормировочный множитель
. Используя это условие, определите
нормировочный множитель ![]() . Ответ:
. Ответ: ![]()
5. Функция
состояния некоторой частицы имеет вид 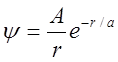 , где
, где ![]() - расстояние этой частицы до силового
центра;
- расстояние этой частицы до силового
центра; ![]() - некоторая постоянная. Определите среднее
расстояние частицы до силового
центра. Ответ:
- некоторая постоянная. Определите среднее
расстояние частицы до силового
центра. Ответ: ![]()
6. Волновая
функция, описывающая основное состояние электрона в атоме водорода, имеет вид ![]() , где
, где ![]() -
расстояние электрона от ядра,
-
расстояние электрона от ядра, ![]() - первый боровский
радиус. Определите среднее значение квадрата расстояния электрона до ядра в основном
состоянии.
Ответ:
- первый боровский
радиус. Определите среднее значение квадрата расстояния электрона до ядра в основном
состоянии.
Ответ: ![]()
7. Волновая функция,
описывающая основное состояние электрона в атоме водорода, имеет вид ![]() , где
, где ![]() -
расстояние электрона от ядра,
-
расстояние электрона от ядра, ![]() - первый боровский
радиус. Определите наиболее вероятное расстояние электрона до ядра.
- первый боровский
радиус. Определите наиболее вероятное расстояние электрона до ядра.
Ответ: ![]()
8. Частица в
одномерной прямоугольной потенциальной яме шириной ![]() с
бесконечно высокими «стенками» находится в возбужденном состоянии (
с
бесконечно высокими «стенками» находится в возбужденном состоянии (![]() ). Определите, в каких точках ямы (
). Определите, в каких точках ямы (![]() ) плотность вероятности обнаружения
частицы: 1) максимальна; 2) минимальна. Поясните полученный результат
графически.
) плотность вероятности обнаружения
частицы: 1) максимальна; 2) минимальна. Поясните полученный результат
графически.
Ответы: 1) ![]() ;
; ![]() ;
; ![]() ; 2)
; 2) ![]() ;
; ![]() .
.
9. Атом водорода
находится в состоянии 1s. Определите
вероятность пребывания электрона в атоме внутри сферы радиусом ![]() , где
, где ![]() -
радиус первой боровской орбиты. Волновую функцию электрона в основном состоянии
считать известной (см. таблицы 1 и 2). Ответ:
-
радиус первой боровской орбиты. Волновую функцию электрона в основном состоянии
считать известной (см. таблицы 1 и 2). Ответ:
![]()
10. Электрон в
возбуждено атоме находится в 3p- состоянии.
Определите изменение его орбитального механического и магнитного моментов при
переходе в основное состояние. Ответ:
![]() Дж/Тл
Дж/Тл
11. Определите
возможные значения проекции ![]() орбитального момента
импульса электрона в атоме на направление внешнего магнитного поля. Электрон
находится в
орбитального момента
импульса электрона в атоме на направление внешнего магнитного поля. Электрон
находится в ![]() состоянии.
состоянии.
12. Электрон
находится в бесконечно глубоком одномерном потенциальном ящике шириной ![]() . Вычислите
вероятность того, что электрон, находящийся в возбужденном состоянии (
. Вычислите
вероятность того, что электрон, находящийся в возбужденном состоянии (![]() +, будет обнаружен в средней трети
ящика. Ответ:
+, будет обнаружен в средней трети
ящика. Ответ: ![]()
13. Почему при физической интерпретации волновой функции говорят не о самой функции, а о квадрате ее модуля?
14. Докажите,
что если ![]() - функция циклически зависит от времени [то
есть
- функция циклически зависит от времени [то
есть 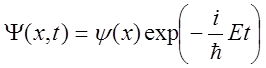 ], то плотность вероятности есть функция
только координаты.
], то плотность вероятности есть функция
только координаты.
15. Покажите,
что собственные функции 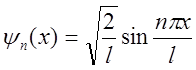 и
и 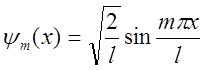 , описывающие состояние частицы в
потенциальном ящике, удовлетворяют условию ортогональности, то есть
, описывающие состояние частицы в
потенциальном ящике, удовлетворяют условию ортогональности, то есть
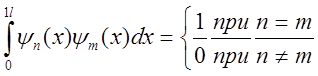 .
.
16. Определите для электрона, находящегося в атоме водорода в 2s- состоянии: 1) расстояния от ядра, на которых вероятность обнаружить электрон имеет максимум; 2) расстояния от ядра, на которых вероятность нахождения электрона равна нулю. Каковы значения орбитальных механического и магнитного моментов, какие значения могут принимать их проекции на направление внешнего магнитного поля? Каковы спиновый механический и магнитный моменты электрона в этом состоянии? Каковы возможные проекции спиновых моментов электрона? Каковы гиромагнитные отношения для орбитальных и спиновых моментов электрона?
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.