Трудности и противоречия классической теории излучения. Гипотеза квантов Планка. Уравнение для определения собственного состояния оператора физической величины. Стационарное уравнение Шредингера для водородоподобных систем. Эффект Штарка, его квантовомеханическое описание

1. Трудности и противоречия классической теории излучения. Квантовые свойства электромагнитного излучения. Гипотеза квантов Планка.

Центральное место в теории строения атома занимает проблема испускания и поглощения электромагнитного излучения, поскольку именно излучение доставляет исследователю наибольшую информацию о внутреннем устройстве атома. На рубеже XIX-XX веков процессы испускания электромагнитного излучения атомами описывались в рамках классической электродинамики. Согласно классической электродинамике, ускоренно движущийся заряд излучает электромагнитные волны. Вращающийся относительно ядра электрон имеет ускорение, а потому должен непрерывно излучать. Теряя энергию на излучение, электрон непрерывно приближался бы к ядру и, в конце концов, упал бы на него. При этом частота обращения, а следовательно, и частота испускаемого электромагнитного излучения должны непрерывно возрастать, то есть спектр атома должен быть непрерывным.

Следовательно, модель Резерфорда в рамках классического рассмотрения не только не объясняет линейчатого характера атомных спектров и закономерностей в них, но и практически отвергает стабильность атома. Не согласующийся с опытом вывод о неустойчивости атома есть результат применения классической физики к явлениям микромира. Решение проблем, связанных со строением атомных систем и описанием их состояний, было получено только в рамках квантовых представлений. Таким образом, теоретической основой современной физики атома является квантовая механика.

Гипотеза квантов Планка

элементарные излучатели представляют собой осцилляторы, которые могут находиться только в некоторых избранных состояниях, в которых их энергия является целым кратным наименьшего количества энергии :

      , ,. . . . . , . . .;

при излучении или поглощении осцилляторы переходят из одного состояния в другое скачком, минуя промежуточные состояния.

Здесь ,

-частота колебаний осциллятора,

 - постоянная Планка, имеющая размерность действия (Дж·с).

22.Уравнение для определения собственного состояния оператора физической величины. Собственные функции и собственные значения оператора.

В классической механике момент импульса частицы определяется как векторное произведение радиус-вектора частицы на ее импульс :

,

или в проекциях на оси координат:

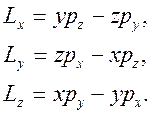
В квантовой механике проекциям момента импульса , ,  ставятся в соответствие операторы

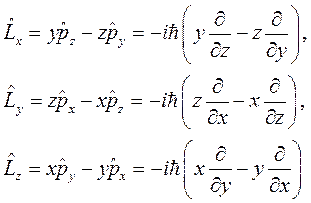                  (6.15)

В сферических координатах выражениям (6.15) соответствуют

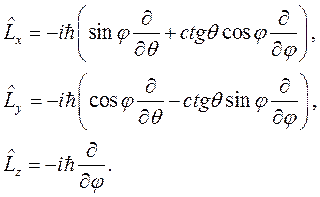                    (6.16)

Собственные функции оператора  определяются из уравнения

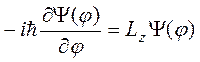
и имеют вид:

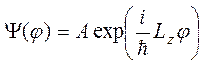.                                 (6.17)

Из требования однозначности функции  следует, что она должна быть периодической с периодом . Тогда

,      0, , , … .               (6.18)

Для операторов   выполняются следующие перестановочные (коммутационные) соотношения:

;       ;       ,     (6.19)

из которых следует, что проекции орбитального момента  связаны соотношениями неопределенностей вида

,

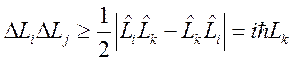
где  и  - неопределенности (дисперсии) измеряемых значений физических величин  и .

Для оператора

                                    (6.20)

с учетом формулы (6.16) можно получить выражение

,                                              (6.21)

в котором

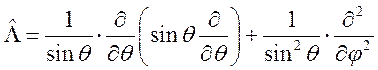           (6.22)

- оператор Лежандра.

Несложно убедиться, что оператор  коммутирует с каждым из операторов :

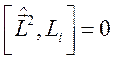;     , , .                       (6.23)

Следовательно, собственные функции операторов   и   одинаковы и могут быть найдены из системы уравнений:

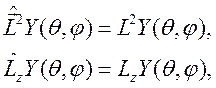                                 (6.24)

записанных в сферической системе координат.

Собственные значения оператора  определяются из уравнения (6.24) в виде

,     1, 2, … .                   (6.25)

При этом собственными функциями для операторов   и   являются сферические функции

,                           (6.26)

образующие полную систему ортонормированных функций (здесь  - присоединенный полином Лежандра, 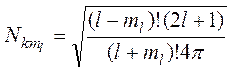 - нормировочный множитель).

23.Стационарное уравнение Шредингера для водородоподобных систем. Алгоритм решения уравнения.

     Решить стационарную квантовомеханическую задачу для системы частиц – значит решить для нее стационарное уравнение Шрёдингера. Решением являются собственные функции оператора Гамильтона, дающие информацию о плотности вероятности обнаружения частицы в любой точке пространства, а также его собственные значения (то есть спектр энергии).

    Простейшими атомными системами являются атом водорода и водородоподобные ионы, то есть такие системы, у которых в поле ядра находится один электрон. Задача о движении электрона в поле ядра интересна сама по себе, кроме того, она имеет фундаментальное значение для атомной физики, так как решение общей задачи о движении электрона в многоэлектронном атоме использует в той или иной мере результаты, полученные для одноэлектронной системы.