На рисунке 4.3 изображено распределение касательных напряжений впереди дислокационного скопления при n = 1 - 3 и x = 5 – 100 Å. Закономерности изменения σxy находятся в соответствии с изменениями скрытой энергии деформации в области неустойчивых состояний кристаллической решётки и сводятся к следующему. При фиксированном значении x и увеличении n количество пиков (в строгом соответствии с n) растёт, причём наблюдается рост их амплитуды. Например, для x = 5 Å максимальное значение σxy 109 Н/м2 составило 14, 15,7 и 15,8 при n равном 1, 2 и три соответственно.
Из приведённых результатов видно, что наиболее интенсивный прирост σxy имеет место при суперпозиции упругих полей двух плоских скоплений; вклад последующих плоских скоплений в общую энергию незначителен. Рассмотрим данные распределения касательных напряжений при удалении от головной части скопления. Величина σxy , характеризующая сдвигообразование и интенсификацию трансляционных перемещений кристаллической решётки, монотонно падает по мере возрастания x для всех значений n, причём падение амплитуды кривых при постоянном значении их интегральной площади влечёт за собой расширение области действия касательных напряжений в направлении координаты у.
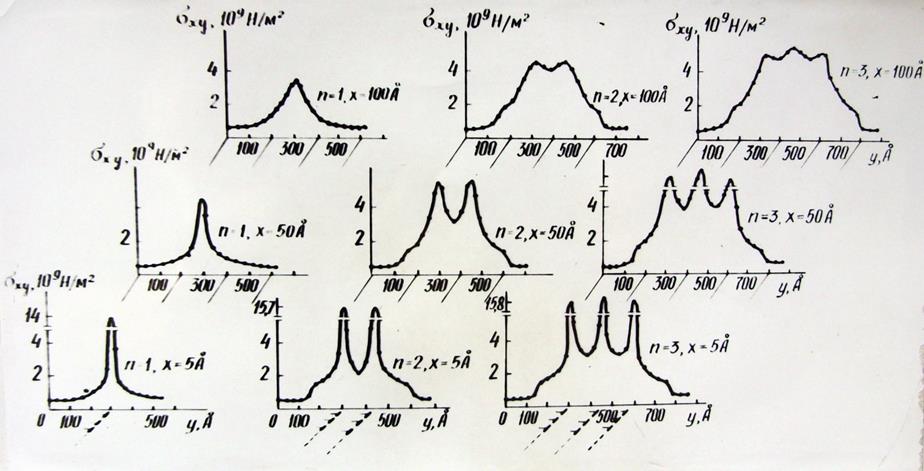
Рисунок 4.3 - Распределение касательных напряжений σxy в головной части плоских дислокационных скоплений
4.3 Распределение знаков нормальных напряжений плоских дислокационных скоплений
Картина распределения знаков σyy плоских скоплений в полосе скольжения приведена на рисунке 4.4 [172]. Для одного плоского скопления картина распределения упругих напряжений следующая: на расстоянии ~ 7,5 Å от ядра головной дислокации в плоскости скольжения лежит резкая граница между напряжениями сжатия-растяжения. Как показывают численные расчеты, на этом интервале перепады напряжения составляют ~ 1019 Па/Å. Рассмотрим упругонапряжённое состояние кристаллической решётки, обусловленное появлением клина σyy. Определим динамику аспектов разрушения в плоскости АВ, параллельной плоскости скольжения и пересекающей границу клина С1Д1 в точке О (рисунок 4.4 вверху). Ввиду того, что слева от n σyy отрицательны (антиколлинеарны n), а справа положительны (коллинеарны n), кристаллическая решётка по линии АВ подвержена влиянию поворотных моментов, обуславливающих микродвижение элементов субструктуры, сопровождающиеся сдвиговой неустойчивостью. Аналогичное действие наблюдается по линии A1B1, находящейся под плоскостью скольжения.
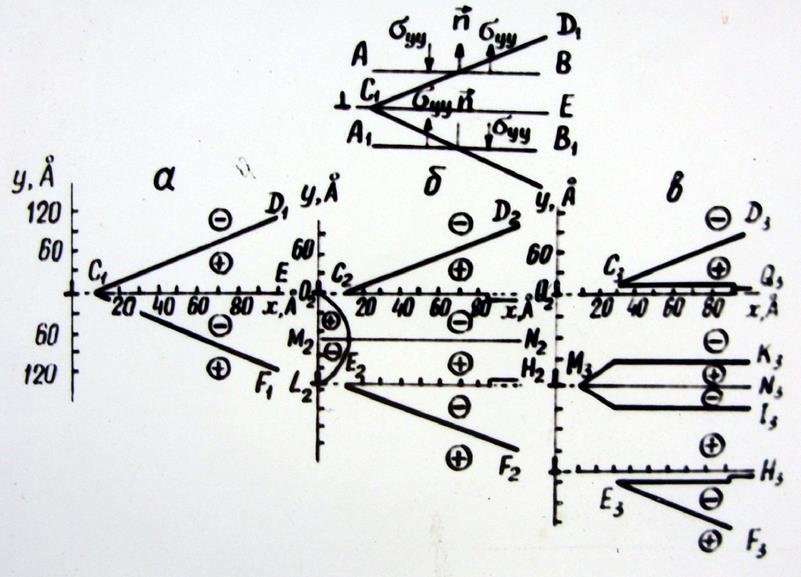
Рисунок 4.4 - Распределение знаков нормальных напряжений в головной части полосы скольжения: a – n = 1; б – 2; в – 3.
Таким образом, рассмотренная модель представляет собой своеобразное раскрытие веера плоскостей с центром вращения в точке C1 (остриё клина). Это обуславливает появление высоких локальных градиентов упругих напряжений, а ограниченная возможность их релаксации путём обычного трансляционного сдвига из-за развитой субструктуры в приповерхностном слое при трении является основным условием развития ротационных мод пластической деформации [173]. В чистых металлах эти условия достигаются при степени деформации ε ≥ 0,3.
Ввиду больших упругих напряжений и их градиентов по линии скольжения C1E стимулируется появление новых и раскрытие существующих микротрещин.
Граница клина является также критической областью при зарождении элементов разрушения в силу асимметрии σyy и больших их градиентов в окрестности границ С1D1, С1F1, а также сложного характера упругих напряжений вдоль плоскости скольжения (рисунок 4.4). Локализация упругих напряжений вдоль границы клина может привести к нарушению сплошности материала и образованию серии зародышевых микротрещин под углом 63º к плоскости скольжения. Этот угол раскрытия оказался весьма близок к его значению при анализе идей Мота, основывающихся на изучении поля напряжений впереди плоского скопления, заторможенного границей зерна [174].
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.