4 Распределение напряжений в полосах скольжения и некоторые структурные предпосылки трещинообразования при трении
Любое разрушение по своей природе является динамическим процессом, в основе которого лежит образование нарушений сплошности цельного материала. Поэтому для выяснения физики процесса разрушения необходимо принимать во внимание, как граничные условия, обусловливающие этот процесс, так и кинетику его развития.
В настоящее время доказано, что формирование источников разрушения (микротрещин) в кристаллической решетке связано с неоднородностью пластического течения, определяемой локализацией деформации и блокировкой скольжения в объеме [3, 158-160].
При фрикционном нагружении процессы трещинообразования должны значительно интенсифицироваться вследствие действия целого спектра физико-химических явлений и локализации пластической деформации в тонких поверхностях слоях. Вследствие этого и особенностей фрикционного нагружения (малости площади и времени силового контакта), а также барьерной роли поверхности для выхода дислокаций [101], накопление скрытой энергии деформации этими слоями будет протекать в условиях скоростного деформирования. Это обстоятельство определяет формирование неоднородной структуры с обилием скоплений дислокаций и повышенной их плотность плотностью [25, 61], что в свою очередь обусловливает качественно отличное (по сравнению с обычными видами нагружения – растяжением, прокаткой и т.д.) сложнонапряженное состояние приповерхностных объемов, предопределяя в них трещинообразование и последующее разрушение. Процессы разрушения стимулируются также образованием устойчивых полос скольжения при трении, в которых концентрируются большие упругие напряжения. Эти полосы формируются обычно при циклическом виде нагружения [161-163], который характерен при трении [164].
В настоящее время нет единого представления о микромеханизмах разрушения поверхностного слоя при трении [1]. Однако установлено, что один из механизмов трещинообразования связан с развитием плоских дислокационных скоплений, создающих локальную концентрацию напряжений впереди головной дислокации скопления [4, 165]. Задачи о распределении этих напряжений до конца не решены.
Исследование полей упругих напряжений дислокационных скоплений, локализованных в полосах скольжения, может помочь решить вопрос о механизмах разрушения приповерхностных слоев в процессе фрикционного нагружения.
4.1 Некоторые структурные предпосылки трещинообразования при трении
В работе [166] рассмотрены силовые аспекты процессов трещинообразования на основе экспериментальных данных, полученных при электронно-микроскопическом исследовании дислокационной структуры никеля при трении. Эти исследования показали, что при фрикционном нагружении в приповерхностном слое формируется своеобразная дислокационная структура с обилием заторможенных групп дефектов и повышенной их средней плотностью. Упругие поля этих скоплений создают критическое упругонапряженное состояние кристаллической решетки, обусловливающее трещинообразование. Этому способствует также наличие на поверхности всевозможных концентраторов напряжений – надрезов, царапин и т.д. Особое значение приобретает проблема ранних стадий протекания этого процесса. Анализируется распределение полей упругих напряжений в головной области плоского скопления дислокаций с последующей интерпретацией данных результатов в полосе скопления. По наблюдаемой части скопления восстановлены параметры всего плоского скопления для решения задачи реализации критического напряженного состояния. Рассмотрено распределение нормальных и касательных напряжений впереди скопления в ортогональных плоскостях. Показано также, что область неустойчивых состояний решетки находится впереди заторможенной полосы на расстоянии ~36 Å.
Для восстановления параметров всего скопления по наблюдаемой части его использовались экспериментальные данные заторможенной полосы дислокационных скоплений, наблюдаемой в никеле при фрикционном нагружении (рисунок 4.1).
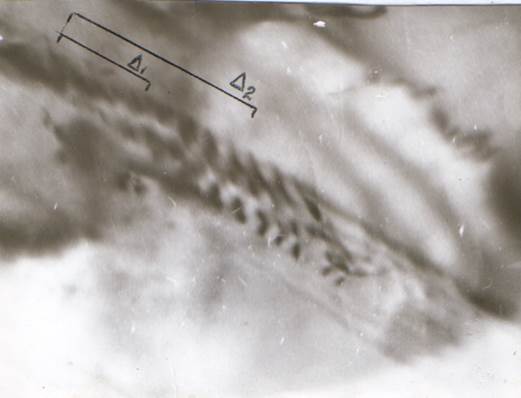
Рисунок 4.1 - Электронно-микроскопический снимок плоского скопления дислокаций в никеле 90000х
Скопления наблюдаются в периоды, предшествующие трещинообразованию. Полоса содержит три плоских скопления, расстояние между которыми составляет ~140 Å. В плоском скоплении для интервала ∆1 = 2*103 Å число дислокаций N∆1 = 11; для ∆2 = 4*103 Å число дислокаций N = 15. Измерение линейных размеров полосы скольжения производилось на измерительном микроскопе ПУОС, включенном в линию ЭВМ “Минск-32” группы обработки фильмовой информации.
4.1.1 Оценка параметров заторможенной полосы скольжения дислокаций
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.