Распределение напряжений в полосах скольжения и некоторые структурные предпосылки трещинообразования при трении, страница 2

В настоящее время при исследовании дислокационного механизма образования трещин используются два способа описания дислокационных скоплений: дискретный [167] и континуальный [168]. Аппарат дискретного метода корректен на начальных этапах развития микротрещин и весьма неудобен для расчета условий зарождения трещин на скоплении [165] . В континуальной теории все величины скопления описываются с помощью функции распределения дислокаций n(x), имеющей смысл плотности вектора Бюргерса b. Эта теория достаточно хорошо описывает поля напряжений от скоплений для расстояний r > b.

В связи с этим мы применили континуальную теорию, так как в области впереди скопления дискретность не проявляется. Распределение дислокаций в одностороннем скоплении длиной l имеет вид [169]:

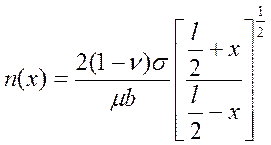                                     (4.1)

Соотношение (4.1) позволяет определить общее число дислокаций в скоплении [169]:

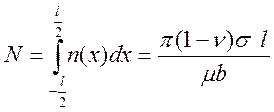                                    (4.2)

Следовательно, для данных σ и N длина скопления может быть представлена в виде:

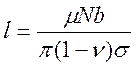                                                 (4.3)

Восстановим параметры скопления (l, N) по наблюдаемой части его (рисунок 4.1).

Число дислокаций в некоторых интервалах ∆I << l согласно выражению (4.2) имеет вид:

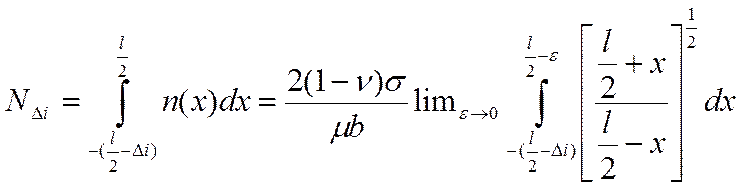
Отсюда следует, что:

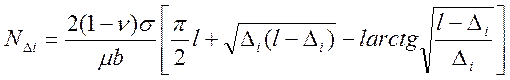                      (4.4)

Учитывая  << l, модно выражение (4.4) привести к следующему виду:

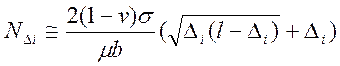                                            (4.5)

Полученная система (4.5) позволяет определить l при i=1,2.

Тогда:

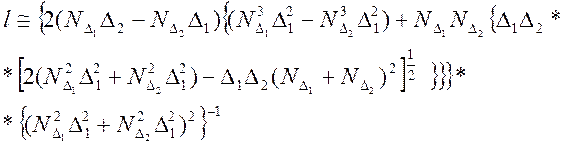               (4.6)

Для оценки воспользуемся одним из уравнений (4.5), тогда

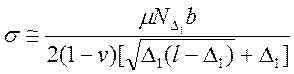,                                                 (4.7)

где l определено согласно формуле (5.6).

Используя выражения (4.6) и (4.7), находим из уравнения (4.2) полное число дислокаций скопления N:

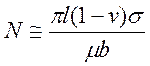                                                                     (4.8)

Эти расчеты получены для плоского скопления дислокаций [166]. Согласно данных работы [170], в параллельных линиях скольжения, составляющих полосу, не происходит существенного перераспределения дислокаций в скоплении. Для условий зарождения трещин впереди полосы скольжения, более сложная полоса будет создавать концентрацию напряжений, близкую к их значению около плоского скопления.

Из выражений (4.6) – (4.8) следует, что параметры полосы скопления имеют следующие значения: l = 372,8*10³ Å;  = 5,27*10⁷ Н/м²; N = 200.

4.1.2 Поле напряжений в головной части скопления дислокаций

Для характеристики упругонапряженного состояния материала оценим компоненты ,и тензора напряжения в головной части плоского скопления дислокаций. В области перед скоплением компоненты тензора имеют вид (система координат связана с головной дислокацией):

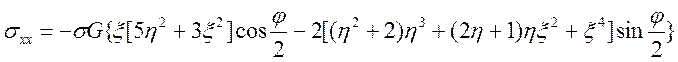,          (4.9)

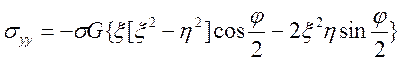,                             (4.10)

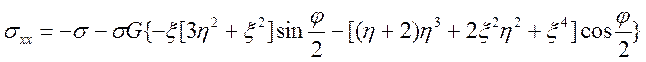,              (4.11)

где , , ,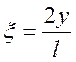

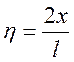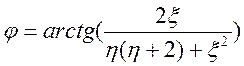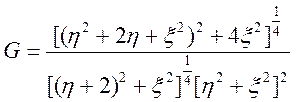
Ограничимся нахождением осевых значений компонент тензора напряжений в полосе скольжения и перпендикулярно к ней (ось х лежит вдоль линии плоского скопления).

Из выражения (4.9) следует (х, 0) = 0.

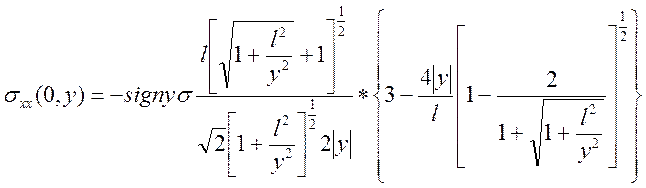               (4.12)

Из выражения (4.12) при y << l

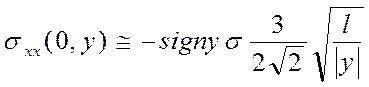,                            (4.13)

а при y >> l

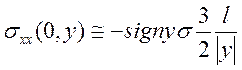                                        (4.14)

Значение компонент тензора напряжения (4.10) при этих же условиях имеет вид:

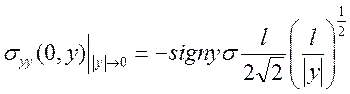                                (4.15)

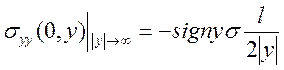                                        (4.16)

С точки зрения различных процессов, происходящих в головной части плоского скопления, наибольший интерес представляют значения осевых, нормальных и касательных напряжений, определяющих формирование микротрещин.

Оценки согласно выражениям (4.15), (4.16) показывают, что по обе стороны от ядра головной дислокации на расстоянии 33 Å реализуются осевые и нормальные напряжения, превышающие теоретическую прочность никеля (9.8*10⁹ Н/м²). По мере удаления от ядра по оси у эти напряжения сначала спадают медленно пропорционально 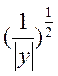, а затем быстро – по закону . При значительном расстоянии (~ 140 Å), когда облегчается безактивационное зарождение трещин за счет влияния соседних плоских скоплений в полосе [165], величины таких напряжений еще достаточно ( = 4,9*10⁹ Н/м²), чтобы зародить микротрещину с учетом факторов, способствующих трещинообразованию при данных условиях фрикционного нагружения (влияние ПАВ, механоциклирование, термоциклирование и т. д.).