ЛАБОРАТОРНАЯ РАБОТА ПММ(2к1с)-06
ПРИМЕНЕНИЕ ЧИСЛЕННЫХ МЕТОДОВ РЕШЕНИЯ
НЕЛИНЕЙНЫХ УРАВНЕНИЙ В ФИЗИЧЕСКИХ ЗАДАЧАХ
Цель работы: 1) применение процедур, реализующих численное решение нелинейных уравнений, для решения физических задач; 2) совершенствование навыков подготовки физических задач для решения на ЭВМ; 3) совершенствование навыков использования подпрограмм.
СОДЕРЖАНИЕ ЗАДАНИЯ
Сформулировать в соответствии с условием варианта нелинейное уравнение f(x)=0 и преобразовать его к безразмерным параметрам. Выделить область изменения аргумента.
Вывод уравнения и его преобразование изложить в отчете.
Используя программу из предыдущей Л.р. в качестве основы, составить новую программу, в которой выполнить:
- построить график функции на заданном интервале с достаточно мелким шагом;
- выбрать по графику начальное приближение корня
- вычислить корень с точностью 10-6 и значение функции в найденной точке.
Записать результаты в отчет.
ВАРИАНТЫ ЗАДАНИЯ
Варианты: 1, 5, 9, 13 - метод половинного деления;
Варианты: 2, 6, 10, 14 - метод хорд;
Варианты: 3, 7, 11, 15 - метод Ньютона;
Варианты: 4, 8, 12, 16 - метод итераций;
1) Плотность тока насыщения при термоэлектронной эмиссии из горячего катода в электровакуумном приборе меняется по закону:
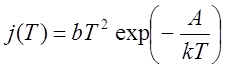 ,
,
где энергия активации А=4,23 эВ; коэффициент b=5,3∙105 А/(м2К2)]; к=1.38∙10-23 Дж/К – постоянная Больцмана. Найти температуру, при которой плотность тока равна 120 мА/мм2.
2) Два положительных электрических заряда величины Q1=4.2∙10-7 Кл и Q2=8.З∙10-7 Кл расположены на оси OY в точках (0,L) и (0,-L), где L=0.25 м. Определить, на каком расстоянии R на оси ОХ величина модуля напряженности поля, создаваемого двумя зарядами, будет равна Е=1000 В/м.
3) Баскетболист бросает мяч с начальной скоростью V0=10,2 м/с. Под каким углом он должен совершить бросок, чтобы попасть в кольцо с расстояния L=8 м по навесной траектории. Высота закрепления кольца Н=2.8м, высота баскетболиста h=1.95 м. Ответ выразить в радианах и в градусах. Указание: описать движение в проекциях на координатные оси x(t), y(t)и, исключив время t, найти уравнение траектории движения у(х).
4) Последовательно соединены резистор из металлической проволоки
и полупроводниковый резистор. Температурные зависимости их сопротивлений
соответственно определяются формулами ![]() ;
; 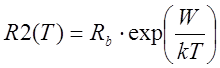 , где Ra
=125 Ом; Rb=5.86∙10-2 Ом;
α=4,18∙10-3 1/К; W=4.8∙10-20 Дж; k=1,38∙10-23 Дж/К. Определить, при какой
температуре общее сопротивление будет минимальным. Указание: положение
минимума можно определить из равенства нулю первой производной, причем она в окрестности
этой точки должна возрастать (вторая производная >0).
, где Ra
=125 Ом; Rb=5.86∙10-2 Ом;
α=4,18∙10-3 1/К; W=4.8∙10-20 Дж; k=1,38∙10-23 Дж/К. Определить, при какой
температуре общее сопротивление будет минимальным. Указание: положение
минимума можно определить из равенства нулю первой производной, причем она в окрестности
этой точки должна возрастать (вторая производная >0).
5) Для резисторов, описанных в предыдущей задаче, найти температуру, при которой их параллельное соединение будет иметь максимальное сопротивление. Указание: положение максимума для r(T) можно определить из равенства нулю первой производной, причем она в окрестности этой точки должна убывать.
6) Электрон влетает в однородное электрическое поле плоского конденсатора с напряженностью Е=880 В/м, имея начальную скорость V0=7.2∙105 м/с, направленную под углом φ к пластинам, длина которых L=10 см. Начальная высота электрона над нижней пластиной, заряженной положительно, равна h0=0.6 см, а при вылете из поля - равна h=0.4 см. Вычислить угол φ. Ответ выразить в радианах и в градусах. Указание: описать движение электрона в проекциях на координатные оси x(t), y(t) и, исключив время t, найти уравнение траектории движения у(х).
7) Снаряд вылетает из пушки под углом α=38° к горизонту с начальной скоростью 345 м/с. Через какой промежуток времени его расстояние (не проекция!) от точки выстрела будет равно 2,5 км. Сопротивление воздуха не учитывать.
8) Электрон, имея скорость 104 м/с, влетел в однородное магнитное поле с индукцией В=30 мТл под углом α к направлению линий индукции. Чему равен угол α, если через время t=0.0001 сек расстояние электрона от начальной точки составило 1,2мм.
9) Наклонная плоскость, образующая угол α с плоскостью горизонта, имеет длину L=2 м. Тело, двигаясь равноускоренно соскользнуло с этой плоскости за время t=2 с. Найти угол α, если коэффициент трения kтр=0,28.
10) Снаряд, выпущеный из зенитного орудия вертикально вверх со скоростью V0=850 м/с, поднялся до высшей точки траектории за время t=38,76 с. Считая силу сопротивления воздуха пропорциональной скорости, определить массу снаряда. (Указание: сформулировать и решить аналитически уравнение движения снаряда).
11) Моторная лодка массой m=420 кг, начинает двигаться по озеру и через время t=18,5 с приобретает скорость V=7,2 м/с. Сила тяги F мотора равна 0,2 кН. Считая силу сопротивления Fсопр движению пропорциональной скорости, определить коэффициент сопротивления. (Указание: сформулировать и решить аналитически уравнение движения лодки).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.