Прямой и обратный метод прогонки. Конечно-разностные производные для граничной задачи ОДУ-2

СУРС №12    Выполнил студент гр.Ф-31 Сорокин Е. А.

                                 

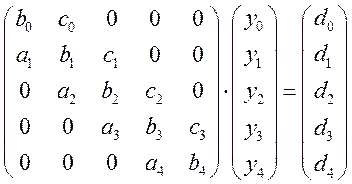
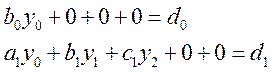
                     2.  Прямой и обратный метод прогонки

      В методе прогонки используются только ненулевые коэффициенты матрицы системы (их можно хранить в памяти компьютера в виде одномерных массивов (векторов)). Метод прогонки основан на том математическом факте, что неизвестные величины с соседними  номерами связаны линейным соотношением:

                                        (14.14)           -неизвестные пока коэффициенты

С учётом этого в методе прогонки выделяются 2 этапа:

а) прямой ход – нахождение всех коэффициентов

б) обратный ход – вычисление всех  на основании (14.14)

      В справедливости соотношения (14.14) можно убедиться непосредственно рассматривая уравнения системы:

                                                         

                                                                

т.е. выполняется                                                   (14.15)

где:        

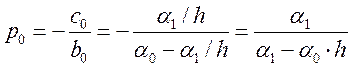
                                                                                                         (14.16)

                             

Рассмотрим первое уравнение

                                                                 

                             

                            

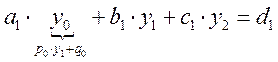
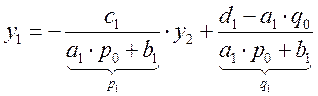                                                      (14.17)

Кроме  того, зная мы можем вычислить .

Получим этот результат в общем виде для i-го уравнения:

                                                                (14.18)

О() показывает оценку отличия конечно-разностных приращений от точной. В численных расчётах этим пренебрегают и используют вместо приращений конечно-разностное выражение:

                 

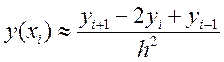
                       3.Конечно-разностные производные для граничной задачи ОДУ-2

              (13.18)

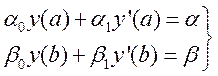                                   (13.19)

Причём  и     (оба коэффициента в нуль не обращаются)

Для решения МКР используем этапы:

1.  Введём сетку на [a;b]                                                             a               h          b

                                                                                       |---|---|---|---|---|---|

                                                                                                                         

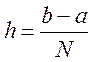
                                     N-число шагов

 Известные функции:    , ….     i = 0…N 

2.  Замена производных на конечно-разностные выражения.

Для внутренних узлов       i = 1…N-1

          

          

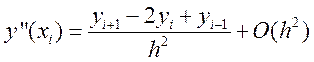
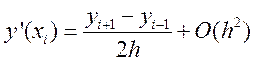
Соответственно в узлах сетки уравнение запишется:

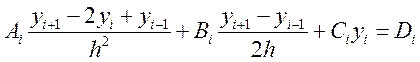                      (13.20)

                                 i = 1…N-1

(13.20) – система N-1 уравнений.