Определение коэффициента Пуассона и частоты биения (Лабораторная работа № 11)

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ПУАССОНА И ЧАСТОТЫ БИЕНИЯ

Цель работы: изучить движение системы со многими степенями свободы, изучить методы определения коэффициента Пуассона, экспериментально определить период биений сплошной колебательной системы и коэффициенты Пуассона.

Приборы и принадлежности: установка, секундомер, весы и разновесы.

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

          Как известно, груз, подвешенный на винтовой пружине, может совершать не только колебательное движение по вертикали, но и вращение вокруг его вертикальной оси. Вращение груза и движение его по вертикали могут происходить одновременно.

          Крутильные колебания вызываются деформацией сжатия (растяжения) продольных слоёв материала пружины, а вертикальные - деформацией сдвига слоёв в поперечном сечении.

          Модуль сдвига N и модуль Юнга E связаны уравнением

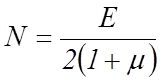                                                                                                               (1)

где - коэффициент Пуассона, т.е. абсолютное значение отношения относительной поперечной деформации к относительной продольной.

          Для пружин с малыми формами наклона витков к горизонтали при их растяжении можно пренебречь деформацией сжатия по сравнению с деформацией сдвига. При закручивании такой пружины можно рассматривать только деформацию растяжения, пренебрегая относительно небольшой деформацией сдвига. Эти обстоятельства дают возможность определить коэффициент Пуассона по измерениям периодов колебаний груза на пружине.

          Из теории упругости известно, что коэффициент жесткости k, винтовой пружины при вертикальных колебаниях груза (без учёта деформации сжатия)

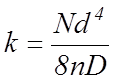                                                                                                                      (2)

          Коэффициент жёсткости  винтовой пружины при крутильных колебаниях груза (без учёта деформации сдвига) равен

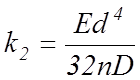                                                                                                                  (3)

где    d  - диаметр проволоки пружины,

          D - диаметр витков пружины,

          n  - число витков пружины,

N и E - соответственно модули сдвига и сжатия.

          Уравнение движения при малых вертикальных колебаниях имеет вид:

                                                                                                                   (4)

а для крутильных колебаний

                                                                                                                   (5)

где    m - масса груза, подвешенного к пружине,

          I  - момент инерции груза относительно оси вращения,

          x - линейное смещение груза при вращательных колебаниях,

          - угловое смещение груза при вращательных колебаниях.

          Из уравнений (4) и (5) можно найти:

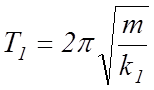                                                  (6)

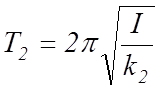                                                                                                               (7)

где     - период вертикальных колебаний,

           - период крутильных колебаний.

          Уравнения (1-3), (6), (7) дают:

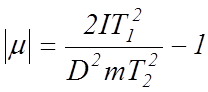                                                                                                        (8)

          Это уравнение можно использовать для определения коэффициента Пуассона материала пружины.

          При более строгом рассмотрении задачи о колебаниях, груз, подвешенный к пружине, необходимо считать системой с двумя степенями свободы. Груз одновременно совершает два вида движения: крутильные и вертикальные колебания. Формально это аналогично движению двух маятников, соединённых между собой лёгкой пружиной. Роль «пружинки» в нашем случае играет связь между деформацией сдвига и деформацией сжатия. Нормальными частотами данной системы являются частоты крутильных и вертикальных колебаний.

          Меняя момент инерции груза путём изменения положения дисков (5) рис.2 относительно оси вращения можно изменить и период крутильных колебаний.

          Если добиться условий, при котором периоды вертикальных и крутильных колебаний мало отличаются друг от друга, можно наблюдать появление «биений», т.е. периодических изменений во времени амплитуды крутильных и вертикальных колебаний.

          Частота биений  равна разности частот двух видов колебаний (крутильных  и вертикальных )

                                                                                                                 (9)

Период биений

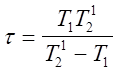                                                                                                           (10)

          Установка (рис.1) состоит из витков пружины 1 с грузом 2 на конце. Груз имеет вид, изображённый на рис.2 и представляет собой цилиндр 3 с двумя одинаковыми симметрично укреплёнными на нём стержнями 4. Для изменения момента инерции груза по резьбе стержней могут перемещаться одинаковые диски 5.