Момент инерции груза относительно оси ОО
![]() (11)
(11)
где ![]() -
момент инерции цилиндра 3,
-
момент инерции цилиндра 3,
![]() - момент инерции стержня 4,
- момент инерции стержня 4,
![]() - момент инерции диска 5.
- момент инерции диска 5.
Для моментов
инерции ![]() ,
, ![]() ,
, ![]() имеем следующие формулы:
имеем следующие формулы:
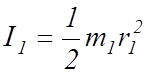 (12)
(12)
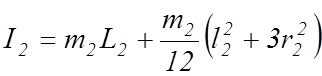 (13)
(13)
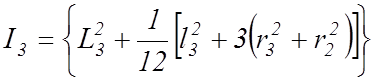 (14)
(14)
где ![]() - масса и
радиус цилиндра 3,
- масса и
радиус цилиндра 3,
![]() -
масса, радиус и длина стержня 4,
-
масса, радиус и длина стержня 4,
![]() -
масса, радиус и толщина диска 5,
-
масса, радиус и толщина диска 5,
![]() - расстояние от оси ОО до центра масс
стержня 4,
- расстояние от оси ОО до центра масс
стержня 4,
![]() - расстояние от оси ОО до центра масс
диска 5.
- расстояние от оси ОО до центра масс
диска 5.
Масса системы m
![]() (15)
(15)
Из (12-14) имеем:
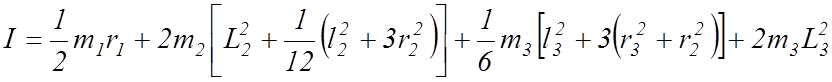 (16)
(16)
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Упражнение 1. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ПУАССОНА
1.
Небольшим опусканием груза
создать вертикальные колебания. Делать это необходимо осторожно, чтобы не сообщить
системе крутильные колебания. С помощью секундомера измеряют время 10-15 полных
колебаний и определяют период ![]() . Опыт
повторить 3-5 раз. Результаты занести в таблицу 1.
. Опыт
повторить 3-5 раз. Результаты занести в таблицу 1.
2. Небольшим поворотом груза вокруг вертикальной оси создать крутильные колебания измерить время 10-15 полных колебаний и определить их период. Следить за тем, чтобы не сообщить системе вертикальных колебаний. Результаты занести в таблицу 1.
3.
Изменяя момент инерции груза,
найти положение дисков ![]() , при котором разность периодов
крутильных и вертикальных колебаний наибольшая. При этом условии найти период
крутильных колебаний
, при котором разность периодов
крутильных и вертикальных колебаний наибольшая. При этом условии найти период
крутильных колебаний ![]() . Опыт повторить 3-5 раз.
Результаты занести в таблицу 2. При изменении момента инерции груза необходимо
следить за тем, чтобы его ось инерции совпадала с геометрической осью цилиндра.
А для этого диски всё время должны находится на одинаковом расстоянии от оси
ОО.
. Опыт повторить 3-5 раз.
Результаты занести в таблицу 2. При изменении момента инерции груза необходимо
следить за тем, чтобы его ось инерции совпадала с геометрической осью цилиндра.
А для этого диски всё время должны находится на одинаковом расстоянии от оси
ОО.
4.
Экспериментальному определению
подлежат величины ![]() . При этом необходимо учесть, что
величина
. При этом необходимо учесть, что
величина ![]() меняется. Для определения массы
меняется. Для определения массы ![]() диск снимают. Значения
диск снимают. Значения ![]() и
и ![]() даны в
конце описания.
даны в
конце описания.
5. По полученным данным, пользуясь формулами (8), (15) и (16) вычислить коэффициент Пуассона. Результаты занести в таблицу 3.
6. Пункты 3, 4, 5, повторить для двух других значений ![]() .
.
7. Найти ошибку определения коэффициента Пуассона.
Упражнение 2. ПРОВЕРКА ФОРМУЛЫ ПЕРИОДА БИЕНИЙ
1. Убедиться, что с уменьшением разности частот при возбуждении крутильных колебаний всё более заметными становятся вертикальные колебания и биения.
2. К проверке формулы (10) приступать при отчётливом наблюдении биений. При этом не следует пользоваться очень близкими значениями частот крутильных и вертикальных колебаний.
3.
При очень малых, осторожно
вызываемых крутильных колебаниях, определить их период ![]() ,
проделав опыт не менее трёх раз. Для периода вертикальных колебаний
,
проделав опыт не менее трёх раз. Для периода вертикальных колебаний ![]() взять значение, полученное в предыдущем
упражнении.
взять значение, полученное в предыдущем
упражнении.
4. Рассчитать период по формуле (10).
5.
Не изменяя момента инерции груза
создать не очень малые вертикальные колебания. Измеряя секундомером время между
двумя последовательными остановками груза при его крутильных колебаниях,
определить период биений ![]() .
.
6.
Определить ошибку измерения ![]() , получив для него не менее трёх значений
по формуле (10) при различных значениях момента инерции системы. При этом
необходимо соблюдать условия, указанные в пункте 2. При этих же значениях
моменты инерции биения находят и экспериментально. Результаты измерений и
вычислений занести в таблицу 4.
, получив для него не менее трёх значений
по формуле (10) при различных значениях момента инерции системы. При этом
необходимо соблюдать условия, указанные в пункте 2. При этих же значениях
моменты инерции биения находят и экспериментально. Результаты измерений и
вычислений занести в таблицу 4.
7.
Сравнить значение периода биений ![]() , полученных теоретически по формуле (10)
со значением периода биений
, полученных теоретически по формуле (10)
со значением периода биений ![]() полученным
экспериментально. Для этого необходимо проверить неравенства:
полученным
экспериментально. Для этого необходимо проверить неравенства:
![]()
![]()
Сделать выводы.
![]()
![]()
Вопросы для самоконтроля
1. Виды деформаций. Их характеристика. Закон Гука. Модуль Юнга. Модуль сдвига (1-4).
2. Коэффициент Пуассона. Вывести формулу (1).
3. Системы со многими степенями свободы. Нормальные частоты. Биения (2,5).
Литература
1. Сивухин Д.В., Общий курс физики, т.1, Наука, 1974 г.,§§ 73,73,75-80.
2. Стрелков С.П., Механика, Наука, М., 1975.,§§ 81-84, 132-134.
3. Хайкин С.Э. Физические основы механики, Наука, М., 1971, гл. XIY, §§ 105-108
4. Петровский И.И. Механика, БГУ Минск, 1973г., гл. YIII, §§1-3.
5. Матвеев А.Н. Механика и теория относительности, Высшая школа, Москва, 1976г., §§ 57,62.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.