Исследование дифракции электромагнитных волн на цилиндре
Цель работы:
Ознакомиться с методами решения дифракционных задач и физическими процессами, происходящими при дифракции плоской волны на идеально проводящем цилиндре. Ознакомиться с методикой измерения напряженности суммарного поля в освещенной области и в области тени.
1. Краткие сведения из теории
Задача дифракции возникает тогда, когда в пространстве кроме источников поля имеется тело или несколько тел. Необходимо найти поле в точке наблюдения (расположенной вне объема, занятого телом), создаваемое заданными источниками с учетом влияния тела. Решение должно удовлетворять граничным условиям на поверхности тела и условию излучения на бесконечности.
Следует заметить, что решение задач дифракции является достаточно сложным. Все методы решения можно разделить на 3 группы:
1) точные (аналитические) методы
2) приближенные методы
3) численные методы
Точные (аналитические) методы пригодны для решения ограниченного круга задач. Примером таких методов является метод собственных функций, который применим только для тел, поверхность которых совпадает с одной из координатных поверхностей в системе координат, где возможно разделение переменных (например, бесконечной длины круговой цилиндр и сфера).
Приближенные и численные методы применимы для более широкого круга задач. С физической точки зрения поле в точке наблюдения можно упрощенно представить как сумму падающего и отраженного полей. Падающее поле создается источниками без учета влияния тела, а отраженное – поверхностными токами, которые наводятся на поверхности тела. При этом наиболее сложным является как раз определение токов на поверхности тела. Если токи известны то по ним можно рассчитать отраженное, а затем и суммарное поле.
Для определения поверхностного тока можно применить приближенные методы
решения. Если дифрагирующее тело представляет собой идеально проводящую
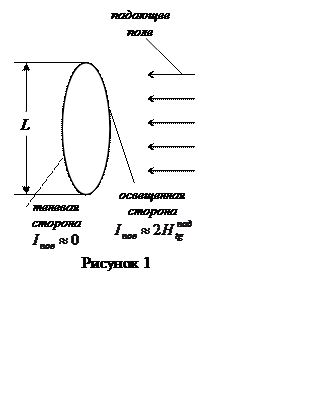
пластину, размер которой L значительно больше длины волны (рисунок 1),
то на освещенной стороне можно приближенно
полагать, что 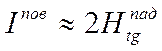 , где
, где ![]() - удвоенная
тангенциальная к поверхности компонента вектора
- удвоенная
тангенциальная к поверхности компонента вектора ![]() падающего
поля, а на теневой стороне поверхности
падающего
поля, а на теневой стороне поверхности ![]() . Такое
приближен
. Такое
приближен
 |
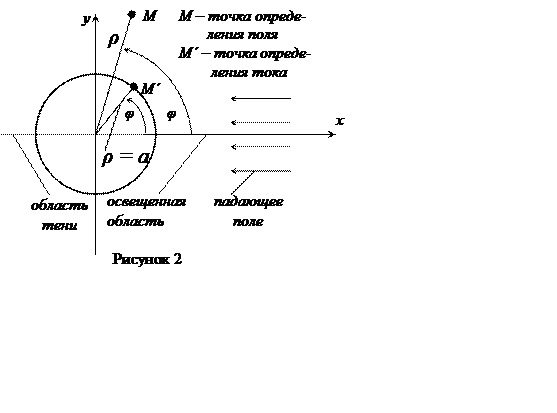 |
1) ![]() || z, падающее поле имеет компоненты
|| z, падающее поле имеет компоненты
![]() и
и ![]() .
.
2) ![]() || z, падающее
поле имеет компоненты
|| z, падающее
поле имеет компоненты ![]() и
и ![]() .
.
Суммарное поле в первом случае должно удовлетворять
граничному условию ![]() , а
во втором случае
, а
во втором случае 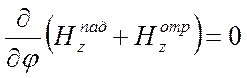 на
поверхности цилинд-
на
поверхности цилинд-
ра.
При решении задачи вводится цилиндрическая система координат ρ,
φ, z. Поскольку для двумерной задачи зависимость от
координаты z отсутствует, точка определения поля имеет координаты ρ
и φ, а точка определения поверхностного тока ![]() и φ (см. рисунок 2). В результате
решения получаем следующие выражения для амплитуды суммарного поля
и φ (см. рисунок 2). В результате
решения получаем следующие выражения для амплитуды суммарного поля
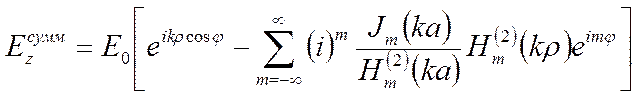 (1)
(1)
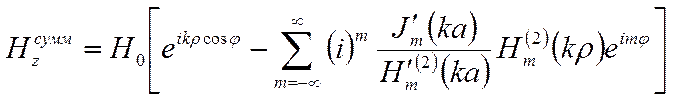 (2)
(2)
Поверхностный ток при этом определяется следующими выражениями
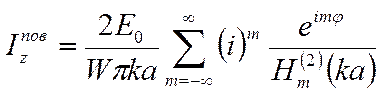 (3)
(3)
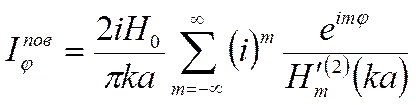 (4)
(4)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.