Исследование дифракции элект­ро­магнитных волн на цилиндре (Отчет по лабораторной работе № 4), страница 2

В (1)–(4) E₀ и H₀ – амплитуды компонент E_z и H_z падающего поля, J_m(ka) и H_m⁽²⁾(ka) функции Бесселя и Ганкеля, a J_m^/(ka) и H_m^(2)/(ka) –их производные.

Выражения (1) и (2) для суммарного поля достаточно сложны для анали­за, поэ­то­му ниже дадимих физическую интерпретацию. Сначала рассмотрим рас­пре­де­ле­ние тока на по­верхности цилиндра, определяемое соотношениями (3) и (4), которое зависит от угла φ, радиуса а и поляризации поля. Анализ выражений (3) и (4) показывает:

1) амплитуда тока максимальна в центре освещенной области () и спадает при приближении φ к 180°.

2) с увеличением радиуса а амплитуда тока с увеличением угла φ спадает быстрее.

3) для || амплитуда тока с увеличением угла φ спадает быстрее, чем для ||.

Типичные графики распределения поверхностного тока приведены на рисун­ках 3 и 4 На этих же рисунках дано распределение тока в приближении фи­зической оп­ти­ки. Видно, что вблизи  распределение тока совпадает с приближением фи­зи­ческой оптики.

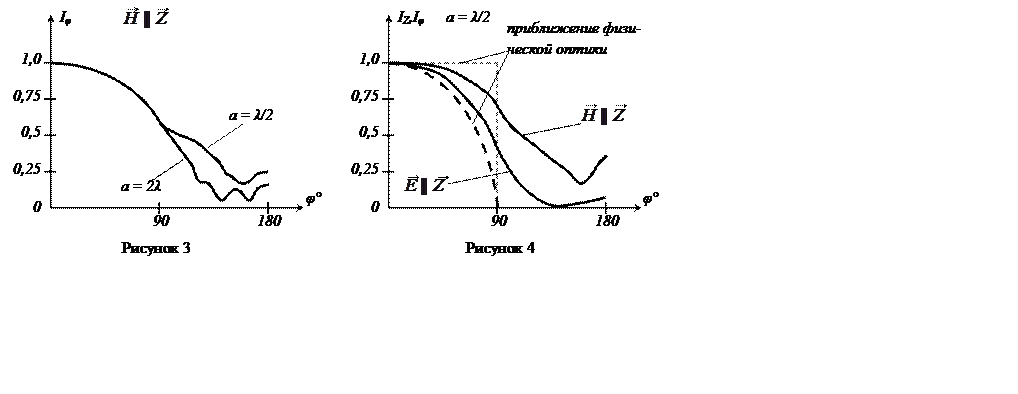
Зная распределение тока можно приближенно определить отраженное, а далее и суммарное поле. Отраженное поле не является плоской волной. В плоской вол­не ам­пли­ту­да поля не зависит от расстояния, а в отраженной вол­не она убывает с уве­личением рас­стояния от поверхности цилиндра. По­скольку отраженное поле соз­дается поверхностными то­ками, оно максималь­но в освещенной области и ми­ни­мально в области тени. Падающее по­ле так­же минимально в области тени, по­сколь­ку оно туда попадает, огибая поверх­ность ци­линдра.

В освещенной области вблизи оси х суммарное поле представляется как сумма па­­да­ющего и отраженного полей, амплитуды которых равны на по­верхности ци­лин­дра (), а по мере удаления от поверхности амплитуда отраженного поля уме­нь­шается. Суммарное поле носит при этом характер стоячей волны (см. рисунок 5). Заметим, если бы вме­сто цилиндра была идеально проводящая плоскость бес­ко­нечных размеров, то от­ра­же­н­ная от нее волна также была бы плоской и в сум­мар­ном поле все максимумы были бы оди­­наковы, а все минимумы равны нулю (см. рисунок 5).

Если рассматривать суммарное поле вблизи оси у, то амплитуда отра­женного поля с увеличением расстояния от цилиндра убывает значительно быстрее. Суммарное поле так­же носит характер стоячей волны, но амплитуда осцилляций ме­ньше, а их период – боль­ше, чем в предыдущем случае. В об­ласти тени амплитуды падающего, отраженного и сум­мар­ного полей значи­тельно меньше, чем в освещенной области. С увеличением радиуса ци­линдра а уменьшение амплитуды проявляется более резко. Амплитуда суммарного по­ля в области тени может быть на несколько порядков меньше, чем в па­дающей плоской во­л­не.

2.  Описание установки и методика из­ме­ре­ний

Установка содержит генератор СВЧ, источник падающего на цилиндр по­ля (пи­­­­рамидальный рупор), два метал­ли­че­с­ких цилиндра радиусом 5 см и 15 см, зонд с детектором, устройство перемещения зо­н­да и индикатор (из­мерительный усили­те­ль). Детектор зонда ориентирован па­рал­ле­ль­но линиям вектора . Блок-схема ус­­та­но­вки приведена на рисунок 6, параметры ус­та­новки выбраны так, что в пло­с­ко­с­ти, в ко­торой перемещается зонд, расп­ределе­ние поля соответствует двумерной за­даче, рассмотренной в разделе 1. При изме­рениях не­обходимо следить, чтобы элек­тро­магнит­ные волны, отраженные от окружающих предметов, не оказывали за­метного влияния на результат. Низкочастотный кабель не до­лжен находится в по­ле падающей и от­ра­женной волны, а если это необходимо - то он ориенти­ру­ет­ся перпендикулярно вектору . Установка позволяет измерить распреде­ление ам­пли­туды суммарного поля в пло­ско­сти, перпендикулярной оси цилиндра, а так­же определить амплитуду суммарного по­ля по отношению к падающему. В пос­лед­нем случае вначале измеряется амплитуда по­ля без цилиндра (падающее поле), а затем амплитуда поля в той же точке при наличии ци­линдра. В ходе этих измерений нельзя изменять выходной сигнал генератора и коэф­фи­ци­ент усиления уси­лителя, можно лишь пользоваться входным делителем напряжения. Ха­ракте­ри­стику детектора при всех измерениях полагаем квадратичной.

Выполнение работы:

ОСВЕЩЕННАЯ ОБЛАСТЬ

F=3150 мГц  λ=9,55 см               Графики распределения поля в освещенной области