Изучение электронно-колебательного спектра поглощения молекулы йода

ИЗУЧЕНИЕ ЭЛЕКТРОННО-КОЛЕБАТЕЛЬНОГО СПЕКТРА ПОГЛОЩЕНИЯ МОЛЕКУЛЫ ЙОДА

Цель работы: Изучить закономерности электронно-колебательных спектров двухатомных молекул, определить характеристики электронно-колебательных переходов молекулы йода.

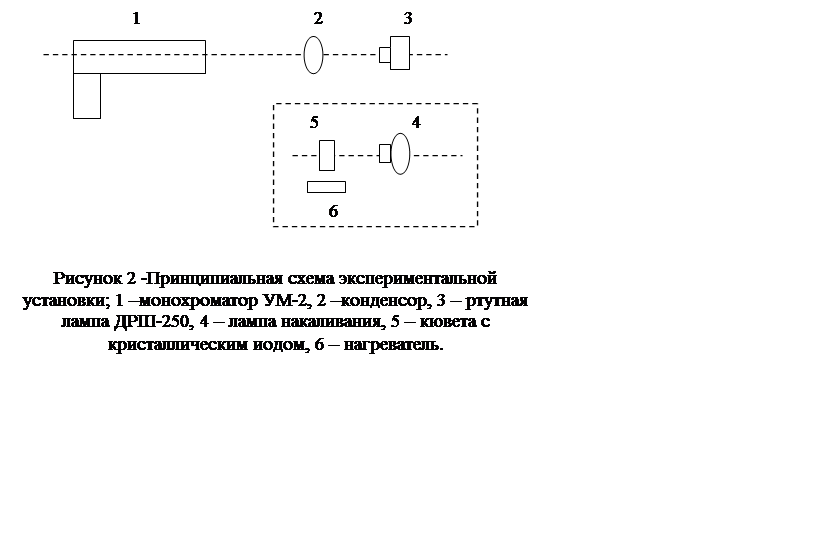
Приборы: Монохроматор УМ-2, ртутная лампа ДРШ-250, лампа накаливания, кювета с кристаллическим йодом, конденсор.

Теоретическое введение

Электронно-колебательные спектры поглощения или излучения молекул располагаются в видимой и ультрафиолетовой области и представляют собой совокупности полос. Полосы обычно имеют резкий край с одной стороны, называемый кантом полосы, и размытый – с другой. При регистрации такого спектра с помощью прибора с высокой разрешающей способностью обнаруживается колебательная структура электронной полосы, анализ которой позволяет определить ряд молекулярных параметров, характеризующих электронное и колебательное движения молекулы.

В данной работе исследуется спектр поглощения двухатомных молекул йода. Этот спектр находится в видимой области и представляет собой серию полос, сгущающихся по мере уменьшения длин волн.

Последовательное описание структуры электронно-колебательного спектра молекул дает квантовая механика. С квантово-механической точки зрения полная энергия молекулы в определенном стационарном состоянии выражается следующим образом:

,                               (1)

где   - энергия электронного движения молекулы (электронная энергия),  - энергия колебательного движения молекулы (колебательная энергия),  - энергия вращательного движения молекулы (вращательная энергия), , ,  - энергии, учитывающие взаимное влияние электронного и колебательного, электронного и вращательного, колебательного и вращательного видов движения молекулы, соответственно.

Электронная, колебательная и вращательная энергии квантованы. Для двухатомной молекулы правило квантования колебательной энергии в ангармоническом приближении имеет вид:

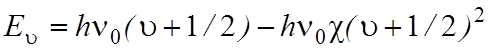,                         (2)

где 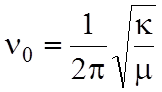 - собственная частота колебания молекулы,  -силовая постоянная химической связи молекулы,  -ее приведенная масса,  = 0,1,2,…. – колебательное квантовое число,  - параметр ангармоничности колебания.

Как видно из формулы (2), с увеличением квантового числа  энергетическая разность между колебательными уровнями уменьшается.

Квантование вращательной энергии двухатомной молекулы имеет вид:

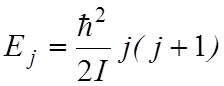,                                                               (3)

где j = 0, 1, 2, 3…; – вращательное квантовое число, I – момент инерции молекулы.

При переходе из одного стационарного состояния в другое могут изменяться все составляющие части энергии молекулы энергия излучаемого или поглощаемого кванта света будет равна:

,       (4)

где один и два штриха, как принято в спектроскопии, относятся к верхнему и нижнему состояниям, соответственно.

Опыт и теория показывают, что . В случае перехода молекул из одного электронного состояния в другое, т.е. в случае электронно-колебательных переходов, не существует строгого правила отбора для колебательного квантового числа , и каждое колебательное состояние верхнего электронного состояния может комбинировать с каждым колебательным состоянием нижнего электронного состояния. Если учесть вращательные переходы, то получим, что каждому электронно-колебательному переходу будет соответствовать полоса, состоящая из большого числа близко расположенных линий.

C учетом вышесказанного частота электронно-колебательного перехода в спектре поглощения (в пренебрежении вращательным движением) на основании формулы (4) определяется следующим образом:

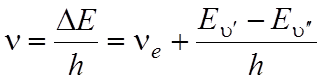,                                                (5)

где 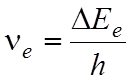 определяет изменение электронной энергии при данном переходе и определяет нулевую линию полосы. Нулевая линия каждой полосы соответствует переходу

Используя (2) и (5), получим, что частоты электронно-колебательных переходов в поглощении могут быть вычислены по формуле:

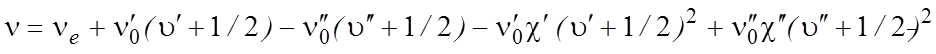(6)

Здесь  ,  - частоты собственных колебаний молекулы в возбужденном  и основном  колебательных состояниях; ,  - параметры ангармоничности колебаний в соответствующих состояниях молекулы.

При невысоких температурах большая часть молекул находится на нижнем колебательном уровне основного состояния . Поэтому при поглощении соответствующих квантов практически имеются только переходы из нижнего колебательного состояния  на различные колебательные уровни верхнего электронного состояния (см. рисунок 1). Если величина колебательного кванта в электронном состоянии невелика или температура достаточно высока, то часть молекул находится в возбужденном состоянии , и поэтому при поглощении могут возникнуть переходы и из первого возбужденного колебательного состояния.

 

При интерпретации экспериментальных спектров сведения о структуре электронно-колебательной полосы молекулы сводятся в таблицу, называемую схемой Деландра. Она имеет вид таблицы, в которую занесены значения частот (волновых чисел) электронно-колебательных компонент полосы.

Определив экспериментально частоты (волновые числа ) электронно-колебательных переходов в спектре поглощения и отнеся их к поперечной серии в схеме Деландра при  = 0, можно, пользуясь формулой (6), определить характеристики молекулы  , а также  ,  ,  молекулы в возбужденном электронном состоянии . Кроме того можно вычислить энергию диссоциации  молекулы в верхнем состоянии, т.е. найти максимальную колебательную энергию молекулы в данном состоянии.

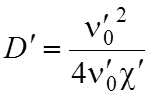.                                                                          (7)

	0	1	2	3	4	….
0
2
3
4
….

Порядок выполнения работы

1.  Изучить оптическую схему и принцип работы установки.

2.  Установить ртутную лампу ДРШ-250 перед монохроматором, включить ее и провести юстировку установки.

3.  Пользуясь атласом спектральных линий ртути, провести градуировку монохроматора, построить градуировочный график.

4.  Установить перед монохроматором лампу накаливания и кювету с кристаллическим йодом, включить подогрев кюветы. Получить отчетливый спектр поглощения молекул йода.

5.  Используя градуировочный график, найти в спектре поглощения йода полосу с длиной волны  = 548,3 нм с квантовым числом =35.

6.  Определить длины волн 5-7 полос поглощения йода, находящихся в окрестности  и занести соответствующие им значения частот в таблицу Деландра

7.  На основании полученных данных рассчитать значения , , , и определить энергию диссоциации молекулы йода в возбужденном состоянии.