КОЛЕБАТЕЛЬНО-ВРАЩАТЕЛЬНЫЕ СПЕКТРЫ ДВУХАТОМНЫХ МОЛЕКУЛ
Цель работы:Изучить закономерности колебательно-вращательных спектров двухатомных молекул, рассчитать значения вращательных констант молекулы на основе ее экспериментального колебательно-вращательного спектра
Теоретическое введение
Молекулы в основном и возбужденном колебательном состояниях распределены по ряду вращательных состояний. При переходе молекулы из одного колебательного состояния в другое одновременно происходит изменение их вращательных состоянии. Поэтому при рассмотрении колебательных переходов необходимо учитывать вращательные состояния. Терм колебательно-вращательного состояния в адиабатическом приближении является суммой термов колебательного и вращательного состояний. В общем случае колебательно-вращательный терм без учета центробежного растяжения имеет вид:
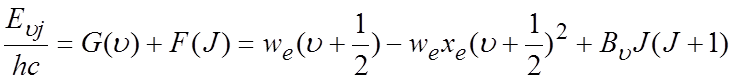
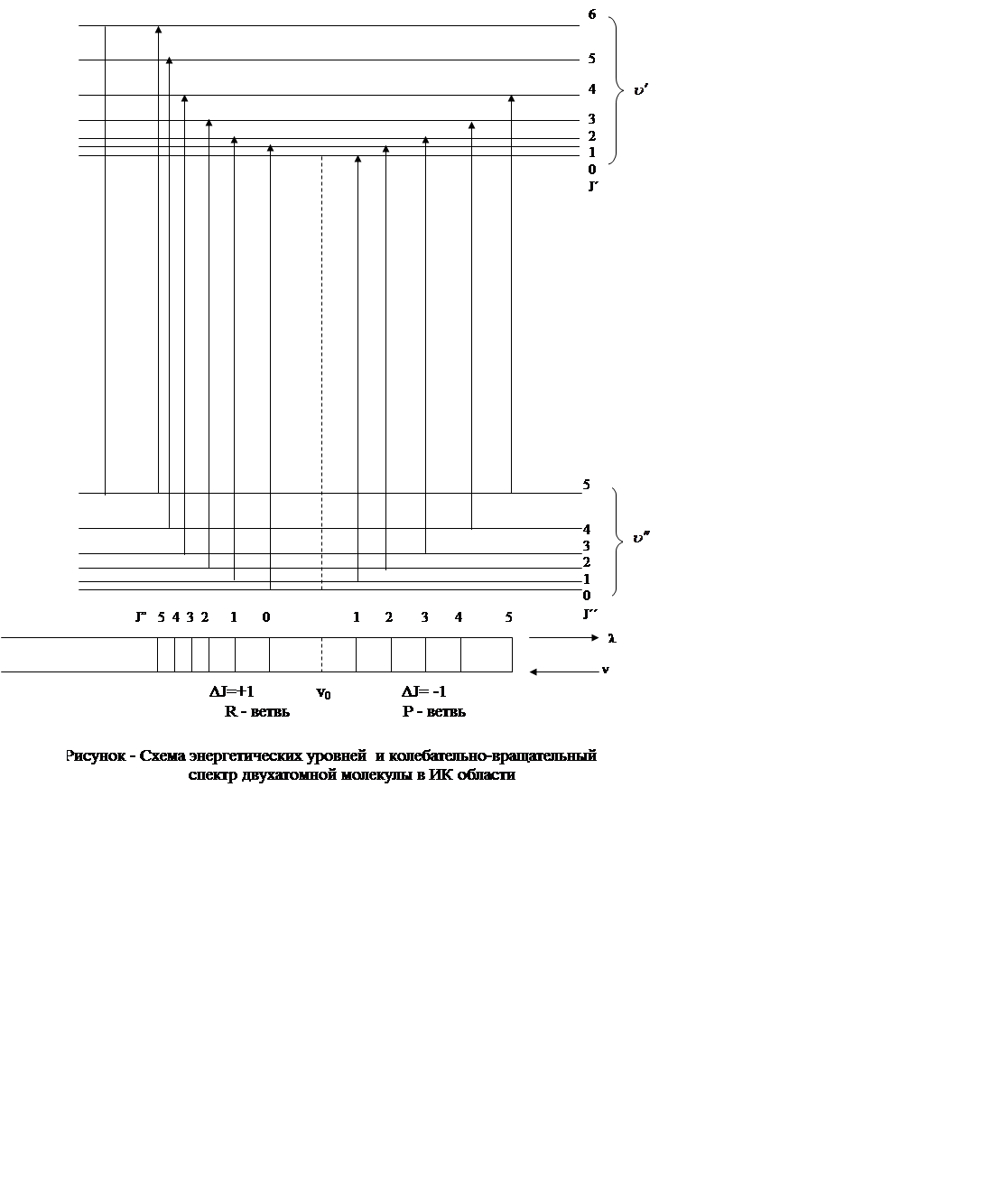
На рисунке 1 приведена система вращательных уровней
для двух колебательных состояний ![]() и
и ![]() . Переходы между уровнями с различными
значениями
. Переходы между уровнями с различными
значениями ![]() и J дают
колебательно-вращательные спектры, для которых правила отбора имеют вид:
и J дают
колебательно-вращательные спектры, для которых правила отбора имеют вид:
по колебательному квантовому числу:
![]() =
±1, ±2, ±3 ...
=
±1, ±2, ±3 ...
по вращательному квантовому числу:
ΔJ =-2, -1, 0, +1, +2
Совокупность переходов, которым соответствуют правила
отбора ![]() сonst,
сonst, ![]() сonst,
образуют ветвь колебательно-вращательной полосы. Приняты следующие
буквенные обозначения ветвей:
сonst,
образуют ветвь колебательно-вращательной полосы. Приняты следующие
буквенные обозначения ветвей:
ΔJ =-2 (О), -1 (P), 0 (Q), +1 (R), +2 (S),
Причем, O,Q,S –ветви проявляются в спектрах комбинационного рассеяния (КР спектрах), а P - и R – ветви активны в инфракрасных спектрах поглощения (ИК спектрах).
Рассмотрим структуру колебательно-вращательной полосы
ИК поглощения (смотри рисунок). В спектре наблюдается две ветви: R –
ветвь (![]() ) , и P – ветвь (
) , и P – ветвь (![]() ), между линиями P и R –
ветвей находится так называемый нулевой промежуток, характеризующийся частотой
ν0 , которая соответствует чисто колебательному переходу
), между линиями P и R –
ветвей находится так называемый нулевой промежуток, характеризующийся частотой
ν0 , которая соответствует чисто колебательному переходу
![]() ,
,
запрещенному
правилами отбора, т. к. для него ΔJ = 0. Отсчет P-линий
начинается с ![]() , а R-линий – с
, а R-линий – с ![]() . Ветвь R всегда
расположена со стороны больших частот от
. Ветвь R всегда
расположена со стороны больших частот от ![]() .
.
Волновые числа линий R- ветви, для
которой ![]() , можно представить уравнением
, можно представить уравнением
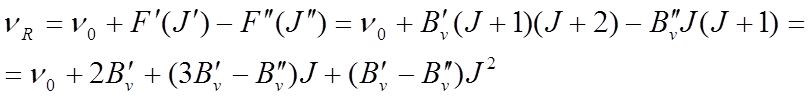
где
вращательное квантовое число ![]() принимает значения
0,1,2,3.
принимает значения
0,1,2,3.
Соответственно для P – ветви, для
которой ![]() , волновые числа
, волновые числа
можно выразить следующим образом:
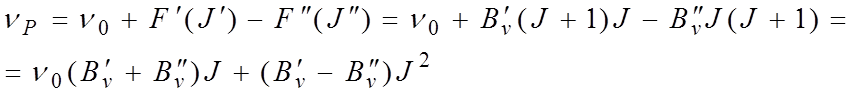
где
![]() принимает значения 0,1,2,3,…..
принимает значения 0,1,2,3,…..
Величина ![]() в случае
колебательно-вращательных всегда имеет отрицательное значение, так как
в случае
колебательно-вращательных всегда имеет отрицательное значение, так как ![]() . Поэтому с ростом значения J
линии вращательной структуры в R-ветви постепенно сходятся, а в P-ветви
- расходятся. Разность (
. Поэтому с ростом значения J
линии вращательной структуры в R-ветви постепенно сходятся, а в P-ветви
- расходятся. Разность (![]() ) мала, поэтому для
малых J в ряде случаев можно пренебречь взаимодействий
колебаний с вращением, приняв
) мала, поэтому для
малых J в ряде случаев можно пренебречь взаимодействий
колебаний с вращением, приняв ![]() . Тогда
. Тогда
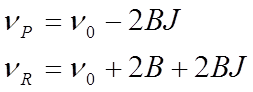
В этом приближении расстояние между двумя соседними линиями вращательной структуры равна 2В, как и в чисто вращательных спектрах.
Для определения вращательных постоянных ![]() и
и ![]() из
колебательно-вращательных спектров используется так называемые комбинационные
разности Δ2F(J), которые представляют собой разность между термами
двумя вращательных состояний, расположенных через один вращательный уровень.
из
колебательно-вращательных спектров используется так называемые комбинационные
разности Δ2F(J), которые представляют собой разность между термами
двумя вращательных состояний, расположенных через один вращательный уровень.
Легко показать, что уравнения
![]()
и
![]()
связаны
с вращательными постоянными ![]() и
и ![]() следующим образом:
следующим образом:
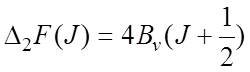
Если для ряда значений …J
вычислить ![]() или
или ![]() то
можно графически или методом наименьших квадратов определить
то
можно графически или методом наименьших квадратов определить ![]() или
или ![]() с
достаточно высокой точностью.
с
достаточно высокой точностью.
Задача 1.
В колебательно-вращательном ИК-спектре поглощение
паров ![]() получен с большим разрешением ряд линий
вращательной структуры, волновые числа которых приведены в таблице (в см-1)
получен с большим разрешением ряд линий
вращательной структуры, волновые числа которых приведены в таблице (в см-1)
|
3108,73 |
3146,09 |
3171,63 |
3193,20 |
|
16,69 |
52,85 |
77,39 |
97,96 |
|
24,40 |
65,52 |
82,91 |
3202,48 |
|
31,87 |
88,19 |
||
|
39,10 |
Определите начало полосы ![]() ,
отнесите линии к ветвям и определите значение вращательного квантового числа
,
отнесите линии к ветвям и определите значение вращательного квантового числа ![]() для каждой линии, отнесите полосу к
основному тону или обертону, сравнить полученное значение
для каждой линии, отнесите полосу к
основному тону или обертону, сравнить полученное значение ![]() с табличным значением we ( Мальцев А.А. Молекулярная спектроскопия, прил. 5). Рассчитайте вращательные
постоянные Bv , Be , αe.
с табличным значением we ( Мальцев А.А. Молекулярная спектроскопия, прил. 5). Рассчитайте вращательные
постоянные Bv , Be , αe.
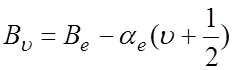
Задача 2.
|
1894,75 |
1864,57 |
1822,93 |
1786,57 |
|
94,17 |
54,01 |
22,40 |
86,16 |
|
87,48 |
56,58 |
14,10 |
77,22 |
|
86,90 |
56,02 |
13,57 |
76,72 |
|
80,02 |
48,42 |
05,12 |
67,61 |
|
79,45 |
47,87 |
04,50 |
67,11 |
|
72,38 |
31,59 |
1795,97 |
|
|
71,81 |
30,95 |
95,45 |
Определите положение нулевой линий ![]() , отнесите линии к изотопическим
модификациям молекул D79Br и D81Br . Сделайте отнесение линий к Р - и R -
ветвям и определите их нумерацию по вращательным квантовым числам J
. Рассчитайте значение вращательной постоянной
, отнесите линии к изотопическим
модификациям молекул D79Br и D81Br . Сделайте отнесение линий к Р - и R -
ветвям и определите их нумерацию по вращательным квантовым числам J
. Рассчитайте значение вращательной постоянной ![]() обеих
изотопических молекул для основного
обеих
изотопических молекул для основного ![]() и возбужденных
и возбужденных ![]() колебательных состояний молекул D79 Br и D81 Br.
Определите молекулярный постоянные
колебательных состояний молекул D79 Br и D81 Br.
Определите молекулярный постоянные ![]() ,
, ![]() и
и ![]() .
Рассчитайте отношение приведенных масс
.
Рассчитайте отношение приведенных масс 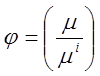 из
молекулярных весов и сравните его с расчетным значением
из
молекулярных весов и сравните его с расчетным значением ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.