ЛАБОРАТОРНАЯ РАБОТА ПММ(2к1с)-07
ИЗУЧЕНИЕ И ПРОГРАММИРОВАНИЕ
ЧИСЛЕННЫХ МЕТОДОВ ИНТЕГРИРОВАНИЯ
Цель работы: изучение и программирование численных методов интегрирования и получения результата с заданной точностью на основе теоретических оценок погрешности.
Рассмотрим практическую задачу. Какой путь пролетел этот объект по прямолинейной траектории, если результаты измерения его скорости следующие:
|
ti |
vi |
|
|
0 |
1.2 |
|
|
0.1 |
1.8 |
|
|
0.2 |
2.6 |
|
|
0.3 |
2.2 |
|
|
0.4 |
1.7 |
Таким образом, задача свелась к вычислению определенного интеграла.
Пусть требуется вычислить определенный интеграл 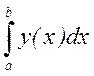 , где y(x) - некоторая заданная на отрезке [а,b]
функция. Известно, что аналитическими методами вычисляется лишь довольно узкий
класс интегралов, поэтому в большинстве практически важных задач возникает
необходимость приближенного вычисления определенного интеграла с помощью ЭВМ,
с заранее заданной точностью ε.
, где y(x) - некоторая заданная на отрезке [а,b]
функция. Известно, что аналитическими методами вычисляется лишь довольно узкий
класс интегралов, поэтому в большинстве практически важных задач возникает
необходимость приближенного вычисления определенного интеграла с помощью ЭВМ,
с заранее заданной точностью ε.
Интеграл для неотрицательных функций f(x) геометрически представляет собой площадь фигуры, сверху ограниченной графиком кривой y=f(x).
Во многих случаях выражение для первообразной не существует, или же подинтегральная функция может быть задана не в виде формулы, а в табличном виде.
В этих случаях подынтегральную функцию заменяют на некоторую интерполирующую функцию, интеграл от которой легко вычисляется в явном виде.
Приближенное вычисление интеграла основано на том, что на малых участках подынтегральная функция заменяется на элементарную функцию с известным поведением, соответствующим поведению интегрируемой функции, и считается площадь, ограниченная сверху графиком этой новой функции. Если отклонения от исходной функции невелики, то невелика и погрешность такого расчета. Формулы приближенного интегрирования различаются между собой выбором приближений.
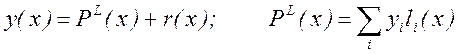
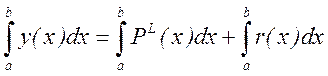
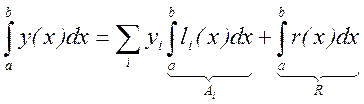
получаем общий вид квадратурной формулы
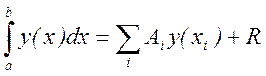
где Ai – весовые коэффициенты, xi – узлы квадратурной формулы, R – погрешность квадратурной формулы.
Квадратурные формулы, полученные на основе интерполяционных полиномов Лагранжа, называются формулами Ньютона-Котеса.
Численное интегрирование применяется, если:
1) подынтегральная функция задана таблицей значений;
2) определенный интеграл не вычисляется в элементарных функциях;
3) подинтегральная функция является громоздкой, сложной для аналитического интегрирования.
В методе прямоугольников подинтегральную функцию приближенно описывают с помощью полинома нулевого порядка – константы.
P0(x) = a = const. Система узлов 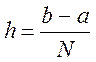 .
.
Метод левых прямоугольников
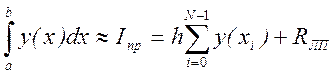
Метод правых прямоугольников
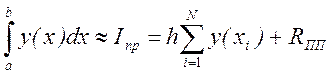
Метод центральных прямоугольников
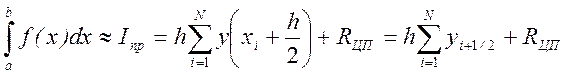
Погрешность методов правых и левых прямоугольников ~h, поэтому эти методы практически не используются в научных и технических расчетах.
Теоретическая оценка погрешности для формулы центральный прямоугольников имеет вид
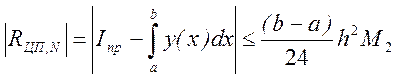 ;
; ![]()
Таким образом, верхний предел погрешности
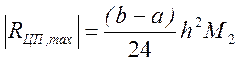
Разобьем интервал [а,b] на N (в общем случае неравных) частей точками x0, x1, x2, … xi, … xN, причем x0=a, xN=b. Обозначим значения подинтегральной функции y=f(x) в этих точках через y0, y1, y2, … yi, … yN, то есть, yi=f(xi). Отметим, что длина интервала разбиения h=(b-a)/N тем меньше, чем больше N.
Рассмотрим малый участок [xi-1, xi], i=1, ... N. Применим к подинтегральной функции линейную интерполяцию, то есть, заменим график функции y=f(x) на отрезке [xi-1, xi] отрезком прямой, проходящей через точки (хi-1, уi-1) и (хi, уi). Площадь получившейся прямоугольной трапеции будет близка к интегралу от заданной функции
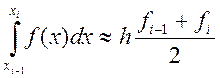
Просуммируем все такие приближенные площади
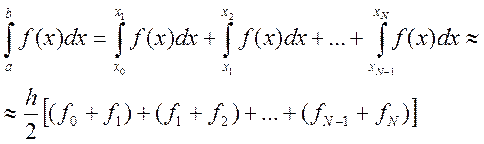
и учтем, что в сумме все значения функции, кроме крайних точек, встречаются дважды. В результате получаем формулу трапеций для расчета определенного интеграла:
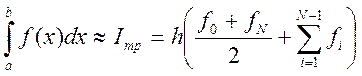
Теоретическая оценка погрешности для метода трапеций имеет вид
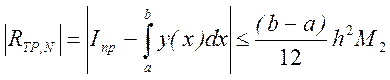
где M2 – максимальное значение модуля второй производной (3.6). Таким образом, верхний предел погрешности
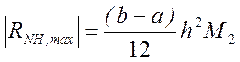
Видно, что теоретически метод центральных прямоугольников вдвое точнее метода трапеций.
Приведем алгоритм расчета по методу трапеций:
Описать функцию y(x)
Задать значения a,b,N
Вычислить h=(b-a)/2
Sum=(y(a)+y(b))/2
Для i от 1 до N-1 выполнять
│ X=a+i*h
│ Sum=sum+y(x)
I=sum*h
Вывод результата I
В этом методе также используется разбиение отрезка интегрирования [а,b] на N равных частей, причем N должно быть четным, так как приближенная формула применяется к каждой паре элементарных отрезков.
Рассмотрим отрезок [xi,xi+2] длины 2h и применим к подинтегральной функции на этом отрезке квадратичную интерполяцию.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.