Информатика и выч. техника \ Программирование и математическое моделирование

Изучение и программирование численных методов интегрирования, страница 2

Проведем через три точки (xi,yi), (xi+1,yi+1), (xi+2,yi+2) пара­болу с осью, параллельной оси OY.

Уравнение этой параболы можно представить в виде (используем интерполяционный полином Лагранжа второго порядка):

где коэффициенты a, b и c находятся из условия, что парабола про­ходит через три заданные точки. На основании условий интерполяции

получаем систему трех уравнений для нахождения коэффициентов a, b, c:

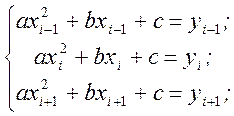
Интегрируя затем непосредственно квадратичную функцию, получим, что площадь под параболой на от­резке [xi,xi+2] равна

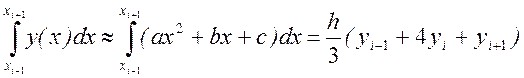
Пусть m=N/2 - число сдвоенных интервалов длины 2h (N – четное). Просуммируем все такие приближенные площади:

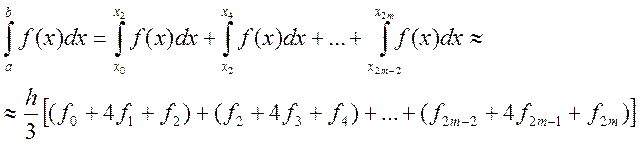
и учтем, что в сумме все значения функции, относящиеся к четным точкам (кроме крайних точек), встречаются дважды. В результате получаем формулу Симпсона для расчета определенного интеграла:

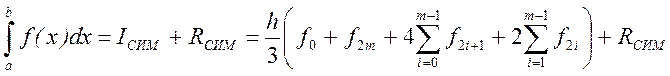
Еще один вариант записи формулы Симпсона:

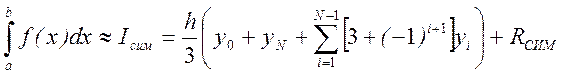
Теоретическая оценка погрешности для метода трапеций имеет вид

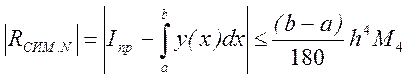
где M4 – максимальное значение модуля четвертой производной (3.6). Таким образом, верхний предел погрешности

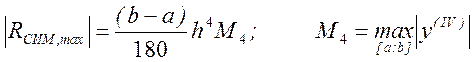
5. Вычисление интегралов с заданной точностью на основании теоретических оценок погрешности

Используя теоретическую оценку максимальной погрешности интегрирования, можно получить, какое число разбиений следует выбрать, чтобы получить результат с требуемой точностью.

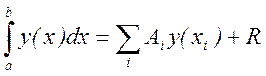
Например, для метода центральных прямоугольников теоретическая оценка максимальной погрешности интегрирования определяется формулой:

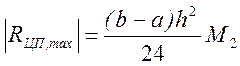
Считая, что эта оценка не должна превышать требуемую точность вычислений, получаем формулы для нахождения максимально возможного шага h (или минимально возможного числа разбиений N)

, →

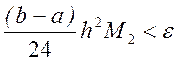
Откуда следует

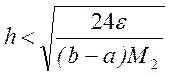
Можно выбрать любое значение h, удовлетворяющее (4.4). Однако следует помнить, что h должно определять согласованную сетку, то есть, на заданной области [a;b] должно помещаться целое число шагов.

С учетом взаимосвязи h=(b-a)/N можно получить формулу для выбора числа шагов

 →

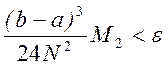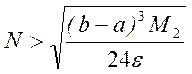
причем значение N следует округлить до ближайшего целого в большую сторону.

Аналогичные соотношения можно получить и для метода трапеций:

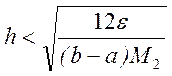 или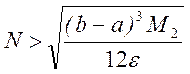

и метода Симпсона

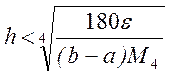 или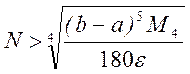

Пример. Вычислить интеграл 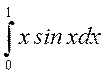 с точностью ε=10-6.

Найдем производные подинтегральной функции

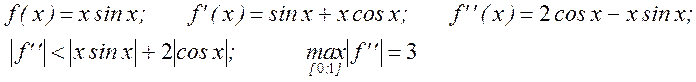
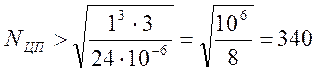
Значит, нужно применить квадратурную формулу (4.4) при N=340, чтобы получить результат с точностью до одной миллионной.

Примечание. Теоретические оценки дают величину максимально возможной погрешности. На практике эти величины могут быть гораздо больше реальной погрешности.

СОДЕРЖАНИЕ ЗАДАНИЯ

ЗАДАЧА 1. Составить программу, содержащую:

-  вычисление подынтегральной функции f(x) в виде подпрограммы-функции;

-  вычисление первообразной функции F(x) в виде подпрограммы-функции;

-  подпрограмму-функцию вычисления определенного интеграла указанным в варианте численным методом. Параметры подпрограммы: пределы интегрирования [a;b] и количество разбиений N:

-  ввод пределов интегрирования и числа разбиений N с клавиатуры;

-  численный расчет заданного определенного интеграла посредством вызова соответствующей подпрограммы-функции;

-  вычисление точного значения определенного интеграла обращением к первообразной функции (контроль точности в тестовом примере);

-  вычисление относительной погрешности численного интегрирования

 .

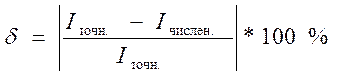Путем многократного выполнения программы получить:

а) значения относительной погрешности при N = 2, 4, 6, .. 20. Построить в отчете таблицу зависимости δ(N).

б) Оценить, при каком значении N относительная погрешность численного результата станет меньше 10-5.

Результаты записать в отчет.

Метод центральных

прямоугольников

Метод

Трапеций

Метод Симпсона

1)

2)

3)

4)  

5)

6)

7)

8) 

9)

10) 

11) 

12)

13) 

14)  

15)

16)

17)

ЗАДАЧА 2. Используя теоретическую оценку погрешности численного метода, найти значение N (и, соответственно, h), обеспечивающее получение результата с точностью ε=10-6. Получить результат и сравнить его с точным. Решение задачи изложить в отчете.

ЗАДАЧА 3. Преобразовать подпрограмму, вычисляющую определенный интеграл, так, чтобы имя подинтегральной функции являлось параметром подпрограммы. Включить подпрограмму в собственный модуль и проверить ее работу.

ЗАДАЧА 4.Преобразовать подпрограмму, вычисляющую определенный интеграл с заданной точностью, так, чтобы имя подинтегральной функции являлось параметром подпрограммы. Включить подпрограмму в собственный модуль и проверить ее работу.

Составил:  Дей Е.А. 2004

Скачать файл