где t - время в течении которого на тело действовала сила F, изменившая импульс тела на величину DR.
Применительно к удару в уравнении (14) F – средняя сила удара,
t - время удара, т.е. время соприкосновения ударяющихся тел, DR=DmV, где m – масса одного из соударяющихся тел (второе тело неподвижно), DV – изменение скорости этого тела, возникающее в результате удара. Если бьющий шар после удара остается в покое, то DV=V, где V – скорость шара в момент удара которая, согласно (10) равна
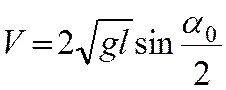 (15)
(15)
Подставив (15) в (14) получаем окончательное выражение для средней силы упругого удара
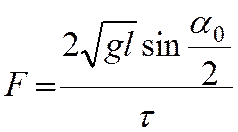 (16)
(16)
ВЫПОЛНЕНИЕ УПРАЖНЕНИЯ.
1. Поместить на нити подвеса шары одинаковой массы и отрегулировать их положение.
2. Измерить время t соударения шаров не менее 10 раз. Результаты занести в таблицу 2 и обработать.
3. Определив длину
подвеса, массу одного шара и значение угла ![]() по
формуле (16), рассчитать среднюю силу удара.
по
формуле (16), рассчитать среднюю силу удара.
Упражнение 3: проверка закона сохранения импульса и определение энергии остаточной деформации при неупругом ударе.
Законы сохранения импульса и энергии при неупругом ударе имеют вид
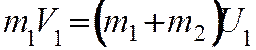 (17)
(17)
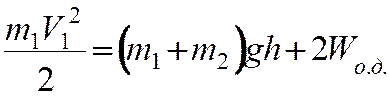 (18)
(18)
где ![]() - масса бьющего
пластилинового шара,
- масса бьющего
пластилинового шара,
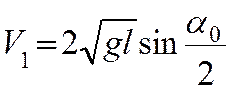 - его скорость в момент удара,
- его скорость в момент удара,
![]() - масса ударяемого
шара,
- масса ударяемого
шара,
![]() - максимальная высота
подъема двух шаров после удара,
- максимальная высота
подъема двух шаров после удара,
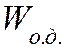 - энергия остаточной
деформации.
- энергия остаточной
деформации.
Учитывая, что
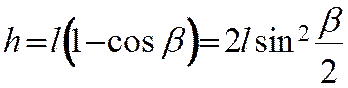
и принимая во внимание выражение (10), вместо (17) и (16) запишем рабочие формулы
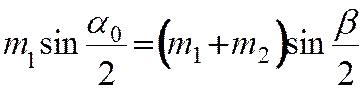 (19)
(19)
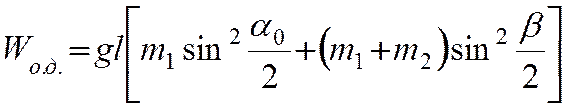 (20)
(20)
где b - угол отклонения шаров после удара.
Упражнение выполняется для одного удара на пластилиновых шарах. Порядок выполнения такой же, как и в упражнении 1. Опыт проделать не менее 5 раз.
Упражнение №1
Проверка закона сохранения импульса и определение коэффициента восстановления упругого удара.
![]() =150
=150
Таблица №1
|
№ |
|
|
|
1 |
0,25 |
8,5 |
|
2 |
0,1 |
9 |
|
3 |
0,25 |
8 |
|
4 |
0,25 |
8 |
|
5 |
0,2 |
8,25 |
|
6 |
0,3 |
8,5 |
|
7 |
0,2 |
9 |
|
8 |
0,25 |
8,5 |
|
9 |
0,15 |
9 |
|
10 |
0,15 |
8,5 |
|
|
0,28 |
8,7 |
|
|
62,255 |
7,507 |
 |
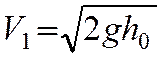 ;
;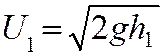 ;
;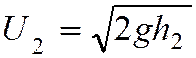
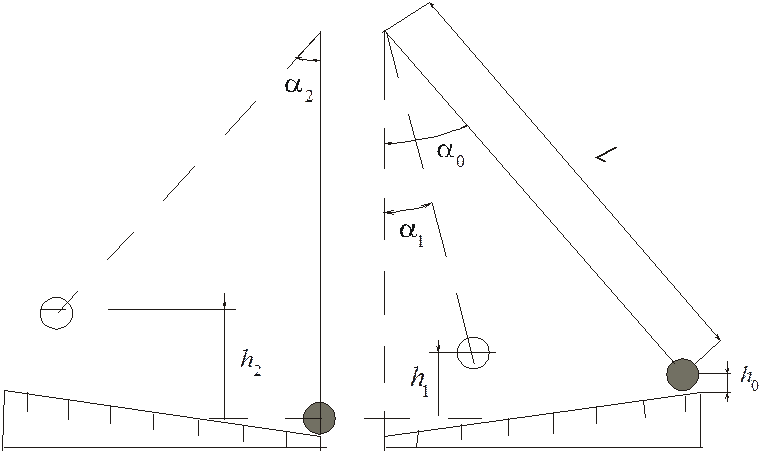
![]() -
высота начального положения ударяющего (правого) шара (рис.2);
-
высота начального положения ударяющего (правого) шара (рис.2);
![]() -
высота, на которую поднимается ударяющий (правый) шар после соударения;
-
высота, на которую поднимается ударяющий (правый) шар после соударения;
![]() -
высота, на которую поднимается ударяемый (левый) шар после соударения.
-
высота, на которую поднимается ударяемый (левый) шар после соударения.
![]() -
скорость правого шара в момент удара;
-
скорость правого шара в момент удара;
![]() и
и ![]() - скорости шаров после удара.
- скорости шаров после удара.
1| 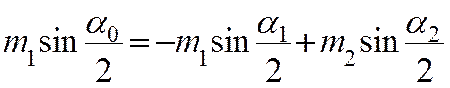
2|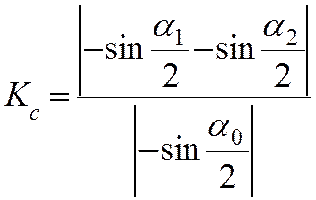
3|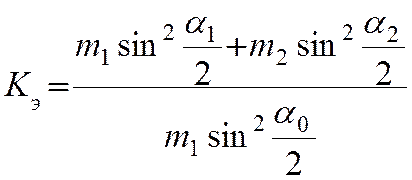
1| 0,106*0.938= –0.106*0,1395+ 0.172*0.935
0.099=0.14
2|Кс=|-0,1395+0.935|/|-0.938|=0.848
3|Кэ=(0,106*0,01946025+0,172*0,874225)/(0,106*0,879844)=1,634
Вывод:
проверил закон сохранения импульса и определил коэффициент восстановления упругого удара
Упражнение 2:определение времени упругого удара и средней силы соударения шаров.
Таблица №2
|
№ |
t (мкс) |
|
1 |
69 |
|
2 |
77 |
|
3 |
75 |
|
4 |
79 |
|
5 |
78 |
|
6 |
72 |
|
7 |
75 |
|
8 |
74 |
|
9 |
78 |
|
10 |
76 |
|
tср |
75 |
l = 47 см = 0.47 см
1)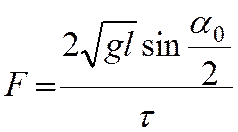 =(2*(9,81*0,47)1/2*0.938)/75=0.053
Н.
=(2*(9,81*0,47)1/2*0.938)/75=0.053
Н.
Вывод:
определил время упругого удара и среднюю силу соударения шаров.
КОНТРОЛЬНЫЕ ВОПРОСЫ.
1. Внутренние и внешние силы.
2. Импульс. Закон сохранения импульса (доказать).
3. Типы удара твердых тел.
4. Количественные характеристики удара твердых тел.
5. Как изменяются кинетическая энергия шаров и их относительная скорость при различных видах удара: абсолютно упругом, неупругом и абсолютно неупругом (доказать).
6. Вывести рабочие формулы.
ЛИТЕРАТУРА
1. Сивухин Д.В. Общий курс физики. т.1, §§10-12, 18, 26, 28, М., 1979.
2. Матвеев А.Н. Механика и теория относительности, М., 1976.
3. Петровский И.И. Механика, Минск, 1973, гл.VI, §§10-12.
4. Савельев И.В. Курс общей физика, т.1, §§22, 23, 30.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.