Физика \ Физика атома и атомных явлений

Запись состояния электронов невозбуждённого атома химического элемента с помощью квантовых чисел. Определение состояния атома, имеющего конфигурацию основного состояния d8 и их расположение по мере возрастания энергии

Страницы работы

6 страниц (Word-файл)
Скачать файл

Содержание работы

Выполнила студентка группы ф-36 Станкевич Светлана

Вариант № 6

Задание 1.

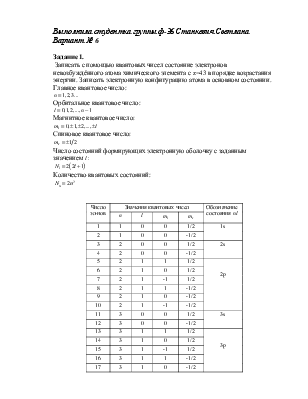
 Записать с помощью квантовых чисел состояние электронов невозбуждённого атома химического элемента с z=43 в порядке возрастания энергии. Записать электронную конфигурацию атома в основном состоянии.

Главное квантовое число:

Орбитальное квантовое число:

Магнитное квантовое число:

Спиновое квантовое число:

Число состояний формирующих электронную оболочку с заданным значением :

Количество квантовых состояний:

Число

эл-нов

Значения квантовых чисел

Обозначение состояния

1

1

0

0

1/2

1s

2

1

0

0

-1/2

3

2

0

0

1/2

2s

4

2

0

0

-1/2

5

2

1

1

1/2

2p

6

2

1

0

1/2

7

2

1

-1

1/2

8

2

1

1

-1/2

9

2

1

0

-1/2

10

2

1

-1

-1/2

11

3

0

0

1/2

3s

12

3

0

0

-1/2

13

3

1

1

1/2

3p

14

3

1

0

1/2

15

3

1

-1

1/2

16

3

1

1

-1/2

17

3

1

0

-1/2

18

3

1

-1

-1/2

19

4

0

0

1/2

4s

20

4

0

0

-1/2

21

3

2

1

1/2

3d

22

3

2

0

1/2

23

3

2

-1

1/2

24

3

2

-2

1/2

25

3

2

2

1/2

26

3

2

0

-1/2

27

3

2

-1

-1/2

28

3

2

1

-1/2

29

3

2

-2

-1/2

30

3

1

2

-1/2

31

4

1

0

1/2

4p

32

4

1

-1

1/2

33

4

1

1

1/2

34

4

1

0

-1/2

35

4

1

-1

-1/2

36

4

1

1

-1/2

37

5

0

0

1/2

5s

38

5

0

0

-1/2

39

4

2

0

1/2

4d

40

4

2

-1

1/2

41

4

2

1

1/2

42

4

2

2

1/2

43

4

2

-2

1/2

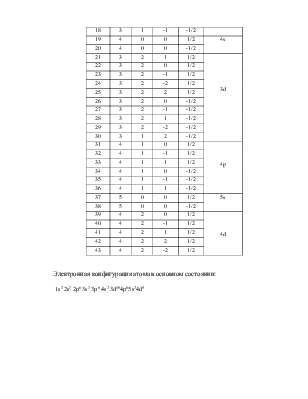
Электронная конфигурация атома в основном состоянии:

 1s2 2s2 2p6 3s2 3p6 4s2 3d104p65s24d5

 

 

 

 

 

 

 

 

 

 

 

Задание 2.  

Определить какие из записанных состояний возможны:


а) 4P1/2   

б) 2G3    

в) 4F3/2

     г) 4D3/2

д) 1S3/2

е) 3D1

ж) 3S1

з) 1H5


L= 0   1   2   3    4    …

     S   P   D   F   G   …

χXJ

       χ=2S-1  -  спиновая мультиплетность

       -условие определяющее возможные значения квантового      числа J


а)  4P1/2                                                                          

L=1

2S+1=4

S=3/2

J= 5/2, 3/2, 1/2

Данное состояние возможно

б) 2G3 

L=4

2S+1=2

S=1/2

J=9/2, 7/2, 5/2, 3/2

Данное состояние невозможно

в)  4F3/2

L=3

2S+1=4

S=3/2

J=9/2, 7/2, 5/2, 3/2

Данное состояние возможно

г)  4D3/2

L=2

2S+1=4

S=3/2

J= 7/2, 5/2, 3/2, 1/2

Данное состояние возможно

д)  1S3/2

L=0

2S+1=1

S=0

J= 0

Данное состояние невозможно

е) 3D1

L=2

2S+1=3

S=1

J= 3, 2, 1

Данное состояние возможно

ж)  3S1

L=0

2S+1=3

S=1

J= 1, 0

Данное состояние возможно

з) 1H5

L=5

2S+1=1

S=0

J= 5, 4, 3, 2, 1, 5

Данное состояние возможно

Похожие материалы

Информация о работе

ВУЗ:
Гомельский государственный университет имени Франциска Скорины (ГГУ им. Скорины)
Предмет:
Физика атома и атомных явлений
Тип:
Контрольные работы
Категория:
Физика (Естествознание)
Размер файла:
171 Kb
Скачали:
0
Скачать файл