Изотопический сдвиг в спектре атомарного водорода

Работа 4. ИЗОТОПИЧЕСКИЙ СДВИГ В СПЕКТРЕ АТОМАРНОГО ВОДОРОДА

Цель работы: измерение разности длин волн для спектральных линий серии Бальмера в спектрах испускания протия и дейтерия, расчет отношения масс дейтрона и протона по спектральным измерениям.

4.1. Учет движения ядра в модели круговых орбит

С помощью модели круговых орбит Н. Бора в работе 3 были получены формулы, в которых радиус орбиты, скорость электрона и полная энергия атома водорода выражаются через фундаментальные константы. При выводе этих формул атомное ядро полагалось неподвижным, что соответствует его бесконечно большой массе. На самом же деле, хотя масса ядра на три порядка превышает массу электрона, при точных расчетах массу ядра нельзя считать бесконечной.

Для учета конечности массы ядра в рамках модели Бора следует принять, что электрон и ядро согласно законам классической механики движутся с одинаковой угловой скоростью вокруг общего центра масс по круговым орбитам (рис. 4.1). При этом радиусы орбит, линейные скорости и центростремительные ускорения будут обратно пропорциональны массам этих частиц:

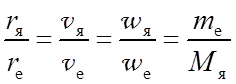                                                 (4.1)

Центростремительное ускорение создается кулоновской силой притяжения электрона и ядра, так что, например, для электрона

(4.2)

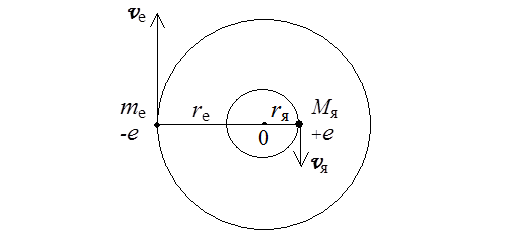
Рис. 4.1

Стационарным состояниям соответствуют те орбиты, для которых момент импульса системы электрон – ядро кратен постоянной Планка ħ:

,

(4.3)

С учетом (4.1) формулам (4.2) и (4.3) можно придать вид:

	(4.2а)
	(4.3а)

Разделив (4.2а) на (4.3а), получим для скорости электрона:

.

(4.4)

Подставив (4.4) в (4.3а), для радиуса электронной орбиты находим

.

(4.5)

При этом расстояние между электроном и ядром r будет несколько больше, чем радиус орбиты электрона r_e :

.

(4.6)

В то же время размеры атома водорода, определяемые величиной

dH = 2 re ,

(4.7)

в силу (4.5) остаются точно такими, как и при бесконечной массе ядра.

Полная энергия атома E равна сумме кинетических энергий электрона и ядра

(4.8)

плюс потенциальная энергия их электростатического взаимодействия

.	(4.9)

Подставляя в формулу (4.8) выражение для v_e из (4.4), а в (4.9) – r_e  из (4.5) и суммируя результаты, получим выражение для энергии стационарных состояний атома водорода:

.

(4.10)

К этому же результату приводит замена массы электрона m_e  на приведенную массу  m  системы электрон – ядро в формуле для E _n, полученной в работе 3 и не учитывающей движения ядра.

.

(4.11)

Если же такую замену произвести в формуле для радиуса орбиты электрона, то изменится ее смысл: это будет формула для расстояния между электроном и ядром.

Вводя энергетическую постоянную А

,

(4.12)

запишем выражение (4.10) для энергии стационарных состояний в виде:

,                    n= 1, 2, 3,…

(4.13)

Если движение ядра не учитывается, то согласно (4.12) при M = ∞, энергетическая постоянная будет равна

.

(4.14)

Подстановка фундаментальных констант в (4.14) дает следующее численное значение постоянной  А_∞ – естественного масштаба энергий в атомной физике:

А_∞=13,605 692 эВ.

Учет движения ядра приводит также к более точному выражению для постоянной Ридберга

;    .

(4.15)

Именно эта уточненная постоянная R входит в обобщенную формулу Бальмера

,      m = 1, 2, 3,… ;  n = m +1, m +2, m +3,…

(4.16)

4.2. Изотопы водорода. Изотопический сдвиг

Наряду с обычным водородом существуют еще два его изотопа, называемых дейтерием и тритием. Ядро атома обычного водорода состоит из одного протона. Такой водород называют протием. Ядро атома дейтерия называют дейтроном, а ядро атома трития – тритоном. Дейтрон состоит из протона и нейтрона, тритон – из протона и двух нейтронов. Эти ядра тяжелее ядра протия приблизительно в 2 и 3 раза, соответственно. Атом протия обозначают через H , дейтерия – через D , трития – через T. Дейтерий – стабильный изотоп, а тритий – радиоактивный. Тритий образуется искусственно при бомбардировке ускоренными дейтронами литиевой или бериллиевой мишени. В ничтожных количествах он образуется также в атмосфере под действием космических лучей. В воде и других природных соединениях на каждые 6800 атомов протия приходится в среднем один атом дейтерия. Благодаря относительно большой разности масс дейтерия и протия различие их физических свойств выражено сильнее, чем для изотопов других химических элементов. Так, плотность тяжелой воды D₂O примерно на 10% больше плотности обыкновенной воды H₂O, а температура плавления D₂O (при нормальном атмосферном давлении) составляет 3,8 ºС.

Различие в массах ядер протия и дейтерия приводит к некоторому различию соответствующих постоянных Ридберга

,

(4.17)

и длин волн спектральных линий. Согласно (4.16), для любой из линий выполняется

,              ,

(4.18)

где   определяется соотношением

.

(4.19)

Различие в длинах волн идентичных линий в спектрах различных изотопов одного и того же элемента называется изотопическим сдвигом. Изотопический сдвиг в спектрах протия и дейтерия хотя и не очень велик, но отчетливо обнаруживается с помощью спектральных приборов среднего разрешения.

Из формул (4.18) легко получить выражение для относительной величины изотопического сдвига для водорода:

.

(4.20)

Видно, что относительная величина изотопического сдвига в рассматриваемом случае одинакова для всех спектральных линий и приближенно равна  m_e /(2 m_p) ≈ 2,7∙10^{– 4}.

4.3. Измерение изотопического сдвига