Работа 14. ШИРИНА Уровней энергии И СПЕКТРАЛЬНЫХ ЛИНИЙ
Цель работы: изучение представлений о естественной ширине уровней энергии и спектральных линий и о причинах их уширения; получение спектрограмм ртути при различных условиях возбуждения, их обработка и оценка вклада различных физических механизмов в уширение спектральных линий.
14.1.Естественная ширина спектральных линий
Классическое рассмотрение. Согласно классической
механике
любое периодическое движение частицы в ограниченной области пространства можно
рассматривать как наложение гармонических движений. Для этого достаточно
представить проекции ![]() её вектора перемещений в виде ряда Фурье, например:
её вектора перемещений в виде ряда Фурье, например:
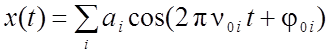 .
(14.1)
.
(14.1)
Здесь ![]() – амплитуда, частота и начальная фаза i-того колебания
(линейного гармонического осциллятора), а частоты
– амплитуда, частота и начальная фаза i-того колебания
(линейного гармонического осциллятора), а частоты ![]() кратны
основной частоте, равной
кратны
основной частоте, равной ![]() , где T – период движения.
Если
частица заряжена, то согласно классической электродинамике при таком движении
она непрерывно излучает электромагнитные волны, которые можно рассматривать как
суперпозицию полей излучения, порождаемых каждым из этих осцилляторов.
, где T – период движения.
Если
частица заряжена, то согласно классической электродинамике при таком движении
она непрерывно излучает электромагнитные волны, которые можно рассматривать как
суперпозицию полей излучения, порождаемых каждым из этих осцилляторов.
Поле излучения отдельного осциллятора представляет собой монохроматическую волну, частота которой совпадает с частотой его движения, а мощность излучения (энергия, уносимая излучением за единицу времени) равна
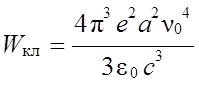 ,
(14.2)
,
(14.2)
где c – скорость света, ![]() – электрическая
постоянная, e – заряд частицы.
– электрическая
постоянная, e – заряд частицы.
Если линейный
гармонический осциллятор обладает в начальный момент времени энергией ![]() и далее не
получает энергии извне, то потери на излучение приводят к затуханию колебаний. При
этом энергия осциллятора убывает по закону
и далее не
получает энергии извне, то потери на излучение приводят к затуханию колебаний. При
этом энергия осциллятора убывает по закону
![]() ,
(14.3)
,
(14.3)
с коэффициентом
затухания ![]() и характерным временем
затухания
и характерным временем
затухания ![]() , для которых
, для которых
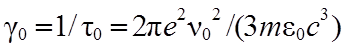 , (14.4)
, (14.4)
где m – масса излучающей частицы.
Затухающие колебания не являются гармоническими (и даже периодическими), и следовательно, излучение не будет строго моно-хроматической волной – оно будет наложением волн с непрерывным набором частот, сосредоточенном в основном в достаточно малом (при слабом затухании) интервале.
Чтобы охарактеризовать распределение интенсивности излучения по частотам
вводят спектральную плотность ![]() , определяемую соотношением
, определяемую соотношением ![]() , где
, где ![]() – мощность излучения в интервале частот
– мощность излучения в интервале частот ![]() . Понятно, что
. Понятно, что 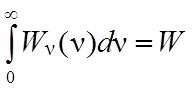 , где W– суммарная
мощность излучения.
, где W– суммарная
мощность излучения.
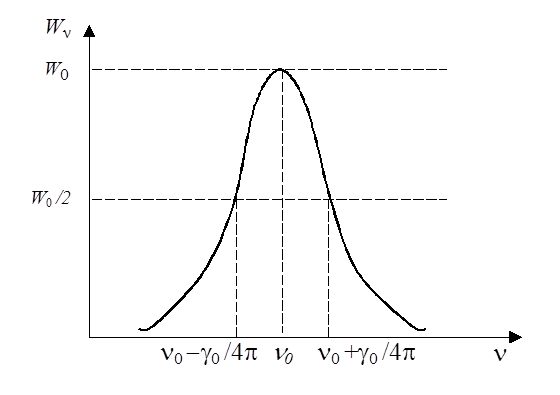
Рис. 14.1
Для спектральной плотности излучения осциллятора с коэффициентом
затухания ![]() и собственной
частотой
и собственной
частотой ![]() , в классической
электродинамике выводится формула
, в классической
электродинамике выводится формула
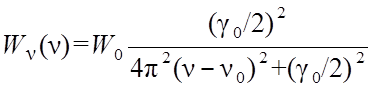 (14.5)
(14.5)
О графике функции ![]() , построенном согласно (14.5), говорят как о естественном
контуре
линии (рис. 14.1). Полушириной спектральной линии называют ширину ее контура при
ординате, равной половине
максимального значения
, построенном согласно (14.5), говорят как о естественном
контуре
линии (рис. 14.1). Полушириной спектральной линии называют ширину ее контура при
ординате, равной половине
максимального значения ![]() . Легко
проверить, что для (14.5) максимум интенсивности
. Легко
проверить, что для (14.5) максимум интенсивности
![]() , равный
, равный ![]() , достигается при
, достигается при ![]() , а ее половинное значение
, а ее половинное значение ![]() – при
– при ![]() .
.
Таким образом, естественная полуширина для контура линии (14.5) составит
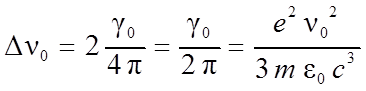 (14.6)
(14.6)
Переходя к длинам
волн согласно соотношению ![]() , получаем
, получаем
![]() , (14.7)
, (14.7)
так что естественная полуширина в шкале длин волн по
классической теории не зависит от частоты ![]() .
.
Как известно, выводы классической теории излучения, прекрасно подтверждающиеся в случае макроскопических явлений, резко противоречат наблюдаемым закономерностям, характерным для излучения атомов. Полное согласие между теорией и экспериментом достигнуто в рамках квантовой электродинамики.
Элементы квантовой теории.Согласно квантовой
теории,
находясь в стационарном состоянии, атом не излучает; электромагнитное излучение испускается или
поглощается при переходе атома из одного стационарного состояния в другое. Частота
этого излучения ![]() определяется разностью энергий
указанных состояний согласно соотношению
определяется разностью энергий
указанных состояний согласно соотношению ![]() . Если
. Если ![]() , то в результате перехода
, то в результате перехода ![]() энергия электромагнитного поля увеличивается
на
энергия электромагнитного поля увеличивается
на ![]() – происходит испускание фотона энергии
– происходит испускание фотона энергии ![]() , а при
, а при ![]() –
поглощение.
–
поглощение.
Поглощение всегда вызвано воздействием на атом, тогда как испускание
может происходить и без явного внешнего воздействия – спонтанно. Вероятность спонтанного
перехода с испусканием за единицу времени с i-того уровня на k-тый – коэффициент
Эйнштейна ![]() – можно вычислить методами квантовой
электродинамики. Если коэффициент
– можно вычислить методами квантовой
электродинамики. Если коэффициент ![]() известен, то легко
найти
число спонтанных переходов с i-того уровня на k-тый для
совокупности одинаковых невзаимодействую-щих друг с другом атомов за время
известен, то легко
найти
число спонтанных переходов с i-того уровня на k-тый для
совокупности одинаковых невзаимодействую-щих друг с другом атомов за время ![]() .
.
Это число равно ![]() , где
, где ![]() – заселенность i-того уровня (число атомов с энергией
– заселенность i-того уровня (число атомов с энергией ![]() ). Отсюда следует, что убыль заселенности i-того уровня за время
). Отсюда следует, что убыль заселенности i-того уровня за время ![]() в результате спонтанных переходов с него на
все нижележащие уровни
определяется суммой
в результате спонтанных переходов с него на
все нижележащие уровни
определяется суммой ![]() по всем
по всем ![]() (рис. 14.2):
(рис. 14.2):
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.