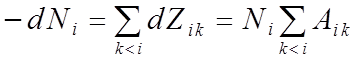Изучение представлений о естественной ширине уровней энергии и спектральных линий и о причинах их уширения, страница 2

.                                    (14.8)

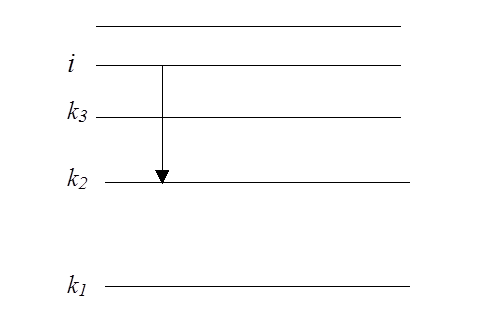
Рис. 14.2

Вводя обозначение для суммарной вероятности спонтанных переходов на все нижележащие уровни 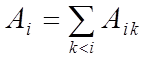 ,  и интегрируя  (14.8),  получаем:

.                (14.9)

Это означает, что возбужденные «стационарные» состояния атома на самом деле являются квазистационарными – обладающими конечным временем жизни, а  имеет смысл естественного (обусловленного спонтанными переходами) среднего времени жизни атома на i-том уровне.

Согласно общим принципам квантовой теории уровень энергии для квазистационарного состояния не строго дискретен, а является квазидискретным – обладает некоторой шириной , связанной с его временем жизни    соотношением

.                                        (14.10)

Следовательно, естественная (обусловленная спонтанными переходами) ширина i-того уровня  определяется вероятностью  :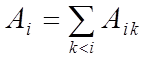

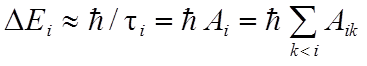.                          (14.11)

Таким образом, в строгом смысле стационарно лишь основное состояние атома, и дискретен лишь его самый нижний уровень энергии.

Понятно, что из-за квазидискретности уровней для частоты излучения, возникающего при переходе между ними, получится не строго определенное значение  , а некоторый интервал частот, характеризуемый величиной

     (14.12)

В квантовой электродинамике доказывается, что контур линии при этом выражается формулой, совпадающей по виду с классической формулой (5), в которую, однако, вместо  следует подставить величину .  Таким образом,

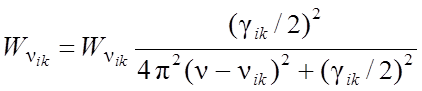                         (14.13)

а формула (12) даёт как раз естественную полуширину спектральной линии в шкале частот. При этом суммарную мощность спонтанного испускания для данного перехода легко получить, умножив число спонтанных переходов за единицу времени    на энергию кванта  :

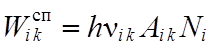                                      (14.14)

14.2. Уширение спектральных линий из-за эффекта Доплера и столкновений

Изложенное выше справедливо в приближении невзаимодействующих между собой покоящихся атомов. Наблюдаемая на опыте ширина спектральных линий излучения макроскопических систем как правило, значительно больше естественной ширины. Рассмотрим два основных механизма дополнительного уширения линий.

Доплеровское уширение. Тепловое движение приводит к тому, что у одной части атомов имеется составляющая скорости , направленная к наблюдателю, а у другой – от наблюдателя. В первом случае будет регистрироваться увеличенная частота, а во втором – уменьшенная. Для разности этих частот получается простое соотношение

                                        (14.15)

Так как средняя кинетическая энергия теплового движения атома равна  , можно принять, что , и сделать оценку для доплеровского  сдвига  частоты:  

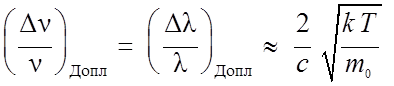                         (14.16)

где  k – постоянная Больцмана,  T– температура,  m ₀– масса атома. Более строгое рассмотрение дает для доплеровской полуширины спектральной линии выражение:

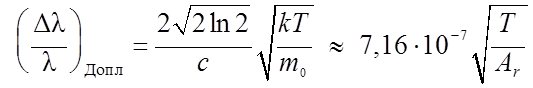             (14.17)

где  A_r– относительная атомная масса.

Уширение из-за столкновений. В результате столкновений время жизни атома на некотором уровне будет (в среднем) ограничено величиной   – средним промежутком времени между двумя столкновениями, которое может оказаться существенно меньшим чем . Соответствующее эффективное уширение уровня энергии можно оценить, исходя из соотношения (14.10): . Из-за уширения уровней произойдет и уширение спектральных линий на величину порядка

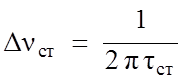                                       (14.18)

Для оценки  заметим, что внутрь воображаемого цилиндра с радиусом основания    и высотой    (рис. 14.3) попадут    центров атомов, где  – эффективный радиус атома, n – концентрация (число атомов в единице объёма). Таким образом, движущийся со скоростью  v  атом за единицу времени испытает в среднем    столкновений, а средний промежуток времени между двумя столкновениями будет равен

.                                      (14.19)

Отсюда, с помощью соотношений  ,  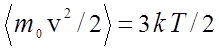,  для газа c температурой  T и давлением  p  получается

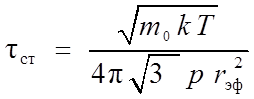                                      (14.20)

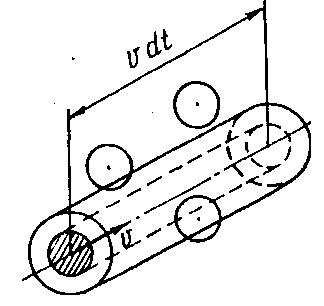
Рис. 14.3

Заметим, что учет движения остальных атомов несколько уменьшил бы полученный результат. Используя (14.18), (14.20) и переходя к длинам волн, получаем оценку для ударного (столкновительного) уширения спектральных линий в газах:

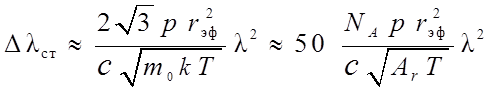                  (14.21)

При использовании формулы (14.21) следует учитывать её оценочный характер и не отождествлять    с газокинетическим радиусом атома.

14.2. Порядок выполнения работы

В данной работе изучается зависимость уширения спектральной линии ртути l = 435,83 нм от условий возбуждения. Исследование проводится для двух источников света: ртутных ламп ПРК- 4 и ДРШ-250, в которых давление и плотность паров ртути существенно различны. В лампе ПРК- 4 давление  р » 1 атм,  в то время как в лампе ДРШ-250 – около 15 атм. Понятно, что во втором случае спектральные линии оказываются более широкими.