Задание 3.
Определить состояние атома, имеющего конфигурацию основного состояния d8 и расположить их по мере возрастания энергии.
В данной задаче до завершения энергетического уровня d8 не хватает двух электронов, поэтому более удобно использовать вместо d8 конфигурацию основного состояния d2 , т.к. d8 эквивалентно d2.
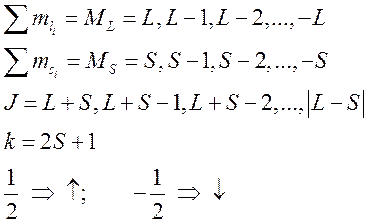
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
↑ |
↑ |
↓↑ |
|||||||
|
1 |
↑ |
↑ |
↑↓ |
↑ |
||||||
|
0 |
↑↓ |
↑ |
↑ |
↑ |
↑ |
|||||
|
-1 |
↑ |
↑ |
||||||||
|
-2 |
↑ |
↑ |
↑ |
|||||||
|
ML |
0 |
1 |
2 |
3 |
2 |
4 |
-1 |
-2 |
-3 |
-1 |
|
MS |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
|
χLJ |
1S0 |
2P210 |
2D321 |
2F432 |
1D2 |
1G4 |
2P210 |
2D321 |
2F432 |
2P210 |
Запишем состояния атома, имеющего конфигурацию основного состояния d2, по мерe возрастания их энергии:
2F234 2D123 2P012 1G4 1D2
Задание 4.
Определить, какие из записанных переходов разрешены правилами отбора:
а) 2D5/2 → 2D3/2
б) 2D1 → 2P0
в) 1G3 → 3D2
г)2D5/2 → 2G7/2
д) 1P1 → 2S1
е) 2D5/2 → 2G5/2
Для перехода должны выполняться следующие условия:
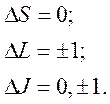
![]() -спиновая мультиплетность
-спиновая мультиплетность ![]() - условие
определяющее возможные значения квантового числа J
- условие
определяющее возможные значения квантового числа J
а) 2D5/2 → 2D3/2
2D5/2
L=2
2S+1=2
S=1/2
J= 5/2, 3/2
Состояние возможно
2D3/2
L=2
2S+1=2
S=1/2
J= 5/2, 3/2
Состояние возможно
Теоретически, данный переход разрешен, так как он удовлетворяет условиям правила отбора. Но практически реализован быть не может, поскольку сами состояния невозможны.
б) 2D1 → 2P0
2D1
L=2
2S+1=2
S=1/2
J= 5/2, 3/2
Состояние невозможно
2P0
L=1
2S+1=2
S=1/2
J= 5/2, 3/2
Состояние невозможно
Теоретически, данный переход разрешен, так как он удовлетворяет условиям правила отбора. Но практически реализован быть не может, поскольку сами состояния невозможны.
в) 1G3 → 3D2
1G3
L=4
2S+1=1
S=0
J= 4
Состояние невозможно
3D2
L=2
2S+1=3
S=1
J= 3, 2, 1
Состояние возможно
Переход не разрешён, так как одно из состояний невозможно
г)2D5/2 → 2G7/2
2D5/2
L=2
2S+1=2
S=1/2
J= 5/2, 3/2
Состояние возможно
2G7/2
L=4
2S+1=2
S=1/2
J= 9/2, 7/2
Состояние возможно
Теоретически, данный переход разрешен, так как он удовлетворяет условиям правила отбора. Но практически реализован быть не может, поскольку сами состояния невозможны.
д) 1P1 → 2S1
1P1
L=1
2S+1=1
S=0
J= 1
Состояние возможно
2S1
L=0
2S+1=2
S=1/2
J= 1/2
Состояние невозможно
Переход не разрешён, так как одно из состояний невозможно
е) 2D5/2 → 2G5/2
2D5/2
L=2
2S+1=2
S=1/2
J= 5/2, 3/2
Состояние возможно
2G5/2
L=4
2S+1=2
S=1/2
J= 9/2, 7/2
Состояние невозможно
Переход не разрешён, так как одно из состояний невозможно
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.