Волновое движение. Звуковые волны в различных средах. Закон Гука. Модуль Юнга. Диаграмма деформации твердого тела. Метод определения модуля Юнга. Упругое последействие. Упругий гистерезис

Тема 12

Волновое движение        

1  Звуковые волны в различных средах

2  Закон Гука. Модуль Юнга

3  Диаграмма деформации твердого тела

4  Метод определения модуля Юнга

5  Упругое последействие. Упругий гистерезис

Основные понятия по теме

Процесс распространения колебаний в какой-либо среде называется волной. В результате распространения волны частицы будут совершать колебания около положения равновесия, при этом происходит передача энергии без переноса вещества. Если колебания частиц происходят в том же направлении, что и распространение энергии, они называются продольными. Если же колебания частиц перпендикулярны к направлению распространения энергии, то такие волны называются поперечными.

Распространяющиеся в сплошных средах упругие волны, воспринимаемые органами слуха человека, называются звуковыми. Их частоты лежат в диапазоне примерно от 16Гц до 20 КГц. Упругие волны с частотой ниже 16 Гц называются инфразвуком, а с частотой от 20КГц до 10⁸ - 10⁹ Гц – ультразвуком.

Для возникновения и распространения звуковых волн необходимо наличие упругой среды (твердое тело, жидкость, газ.). Твердые тела обладают как упругостью объема, так и упругостью сдвига, поэтому в твердых телах звуковые волны могут быть и продольными и поперечными. В жидкостях и газах, которые не обладают упругостью сдвига, могут возникать и распространяться только продольные звуковые волны.

Данные экспериментов по определению скорости звука в различных средах показывают, что она в большинстве случаев не зависит от частоты (или длины волны), т.е. для звуковых волн отсутствует явление дисперсии.

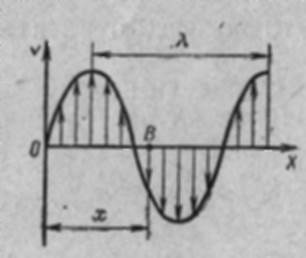
          Уравнение бегущей волны. Рассмотрим процесс распространения колебания, источником которого является точка О (рис.1), колеблю­щаяся гармонически по закону:

                          (1)

    Пусть колебание точки началось в момент времени t=0. Соседние точки придут в колебание с той же амплитудой y₀ и частотой , что и точка О, но с некоторым запаздыванием. Начало колебаний точки В, отстоящей на расстоянии x от источника, отстанет от начала колебаний точки О на время

,

где v — скорость волны в данной среде.

Рисунок 1.

Если величина отклонения точки от положения равновесия в момент времени t равна , то вследствие запаздывания отклонение точки В в тот же момент времени t будет таким же, каким было отклонение точки О на время  ранее, т. е.

или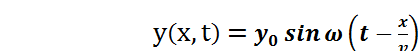                          

Уравнение (2) называется уравнением бегущей волны.

Расстояние, на которое распространяется колебание за один период, называется длиной волны λ:

                                              (3)  

где T – период колебаний. Так как , то уравнение бегущей волны можно переписать в виде:

.

Фазы колебаний точек, отстоящих друг от друга на расстояние λ, совпадают. Поэтому длину волны можно определить как расстояние между ближайшими двумя точками, колеблющимися в одной фазе.

Скорость распространения колебаний можно представить в виде:

,                                                          (4)

где  - частота колебаний.

Из формулы (4) видно, что скорость распространения колебаний можно определить, зная частоту источника  и длину волны . В данной работе скорость звука определяется методом стоячих волн – методом Кундта.

Уравнение стоячей волны. Стоячая волна является результатом интерференции двух одинаковых бегущих волн, распространяющихся навстречу друг другу. Такие волны чаще всего образуются при нало­жении волн, падающих на какое-нибудь тело, и волн, отра­женных от него.

Например, если взять упругий стержень, правый конец которого укреплен неподвижно, а левый периодически сжимать, то образующиеся при этом продольные бегущие волны, достигнув правого конца стержня, отражаются и, распространяясь в обратном направлении, налагаются на волны, исходящие от непрерывно колеблющегося источника. Благодаря этому каждая точка стержня будет одновременно участвовать в двух колебаниях. Результирующее смещение всех точек стержня можно найти путем алгебраического сложения смещений, так как они происходят вдоль одной прямой.

Пусть отражение происходит от среды более плотной, чем стержень. Тогда деформация сжатия, достигшая правого конца, не может привести его в движение. Поэтому за сжатием в падающей волне будет следовать сжатие в отраженной волне, за растяжением в падающей волне — растяжение в отраженной волне. Это приводит к тому, что при отражении от более плотной среды фаза колебания меняется на противоположную (π). Рассмотрим случай, когда отраженная волна имеет ту же амплитуду, что и падающая:

;

.

Результирующая волна:

.             (5)

Уравнение (5) является уравнением стоячей волны. Величина  не зависит от времени и является амплитудой стоячей волны. Точки, в которых амплитуда максимальная, называются пучностями. Точки, в которых амплитуда равна нулю, в колебаниях не участвуют. Такие точки называются узлами.

Расстояние l между соседними узлами можно найти из условия: