Проектирование фундамента промежуточной опоры однопутного железнодорожного моcта (расчетный пролет моста = 33м), страница 6

 2)Определим природное напряжение в уровне подошвы фундамента от собственного веса грунта:

s_zp=s_zg,0=g’×d_n

где g’=10,59 кН/м³ – усредненный по глубине d_n удельный вес грунтас учетом взвешивающего действия воды;

d_n – 4,45 м – глубина заложения фундамента от природной поверхности дна водотока.

3)Определяем избыточное давление над природным среднее давление по подошве фундамента:

P₀=p-s_zg,0

4)Разбиваем грунтовую толщу ниже подошвы фундамента на отдельные слои.

Рис.4.2. Фундамент мелкого заложения

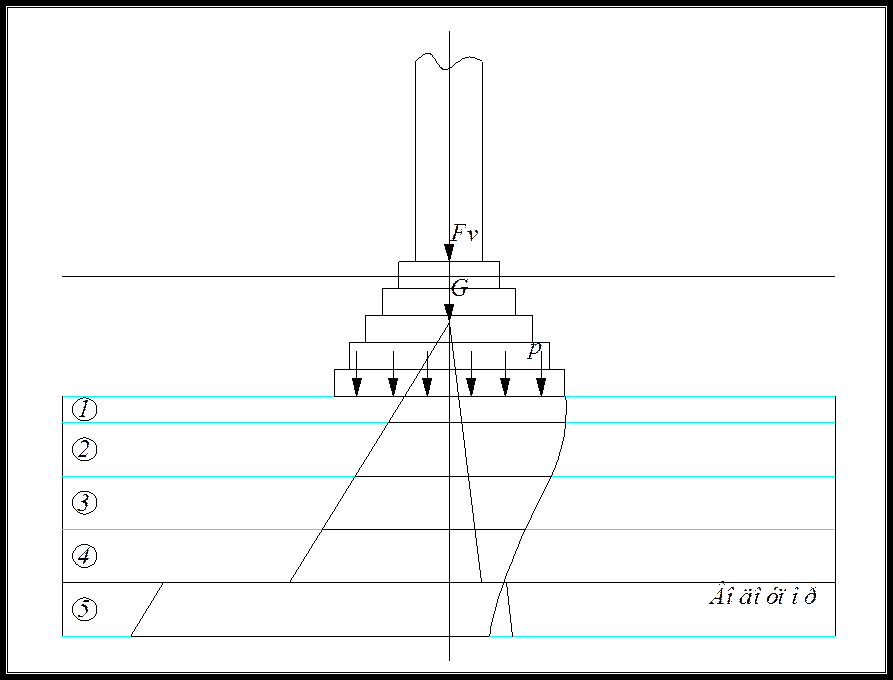
5)Определяем напряжения от собственного веса, лежащего выше грунта на границах выделенных слоев под центром тяжести подошвы фундамента:

s_zg=g’×d_n+Sg_i×h_i

где g_I – удельный вес грунта i-го слоя;

h_i – толщина i-го слоя грунта.

6)Определяем напряжения, дополнительные к природным:

s_zp=a×p₀

где a - коэффициент расеивания напряжений.

7)Определяем среднее в каждом i-ом слое дополнительное напряжение:

s_zp,i=(s’_zp,i+s”_zp,i)/2

где s’_zp,i, s”_zp,i – дополнительные напяжения по верхней и нижней границам i-го слоя.

8)Определяют осадку каждого выделенного слоя от давления s_zp,I по формуле:

S_i=0.8×s_zp,i×h_i/E_i

Где E_i – модуль деформации грунта в i-м слое.

9)Вычисляем полную осадку основания:

S=Ss_i

Табл. 4.3.Осадка фундамента

Номер слоя	Толщина слоя hi, м	Расстояние от границы подошвы фундамента до границы слоя zi, м	Бытовое давление на границе слоя szg, кПа	zi/b	Коэффициент рассеивания напряжений a	Дополнительное напряжение на границе слоя szp, кПа	Среднее давление в i-м слоеszp,i, кПА	Модуль деформации грунта в i-ом слое Ei, МПА	Осадка i-го слоя si, м
1	1	1	73,35	0,122	0,98	139,25	76,96	28	0,002
2	2	3	112,55	0,365	0,86	122,20	72,36	13	0,009
3	2	5	151,75	0,608	0,64	90,94	60,65	13	0,007
4	2	7	190,95	0,851	0,46	65,36	51,78	13	0,006
5	2	9	379,84	1,094	0,34	48,31	62,14	30	0,003
									0,027

10)Расчетная осадка S не должна превосходить предельно допустимую для данного сооружения осадку S_u, которую для опор балочных разрезных мостов рекомендуется применять равной:

S_u=0.001×L₀

где L₀=33 м – длина меньшего пролета примыкающего к опоре.

S_u=0,001×33=0,033 м

0,027 м £ 0,033 м

Проверка выполняется.

4.3.3. Проверки горизонтального смещения верха опор

Горизонтальное перемещение верха опоры определяют по формуле:

u=u_оп+(h_оп+h)×w

Где u_оп=0 м – горизонтальное перемещение верха опоры за счет деформаций изгиба тела опоры и фундамента;

h_оп=9,95 м – высота опоры;

h=5,05 м – высота фундамента;

w - угол поворота фундамента в плоскости моста, определяемый по формуле:

w=(1-n²_m)/E_m×k_b×M/(b/2)³

где k_b=0,48 – безразмерный коэффициент;

n_m- среднее в пределах расчетной зоны сжатия основания значение коэффициента Пуассона:

n_m=S(n_i×h_i)/Sh_i

E_m - среднее в пределах расчетной зоны сжатия основания значение модуля деформации грунтов:

E_m=SA_i/S(A_i/E_i)

Где n_i, E_i, h_i – коэффициент Пуассона, модуль деформации и толщина i-го слоя грунта.

n_m=(0,27×1+0,3×2×3+0,35×2)/(1+2×3+2)=0,31;

E_m=573,82/0,035=16395 кПа;

w=(1-0,31²)/16395×0,48×2145,7/(8,23/2)³=0,001 рад;

u=(9,95+5,05)×0.001=0,015 м.

Горизонтальное смещение верха опоры ограничивается предельно допустимым значением, которое вычисляется как:

U_u=0.5×ÖL₀=0,5×Ö33=2,9см

1,5 см £ 2,9см

Проверка выполняется.

5. ПРОЕКТИРОВАНИЕ СВАЙНЫХ ФУНДАМЕНТОВ

5.1. Общие сведения

В курсовом проекте свайный фундамент и основание  рассчитаны по двум группам предельных со­стояний: