Статистический анализ экспериментальных данных методом наименьших квадратов (Раздел 8 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 6

                                              ,   ,

где  – наблюдаемая величина,  – ошибка наблюдения. Требуется по результатам наблюдения определить оценку величины a с использованием МНК, а также получить характеристики точности оценивания при известных моментных характеристиках ошибки :

                                    ,  ,   .

Данная задача совпадает с задачей из примера 8.1, однако там ничего не говорилось о статистических свойствах ошибок измерения .

▼ Случайную величину  представим в виде вектора

                                               .

Роль вектора оцениваемых параметров играет скалярная величина a,  т.е. k = 1. Поэтому матрица X, имеющая размерность n´k, представляет собой вектор-столбец, состоящий из единиц:

                                                  

В качестве матрицы весов Q выбираем единичную матрицу E_[n]. МНК-оценку скалярной величины a вычисляем по формуле (8.3.12). Предварительно найдём матрицы  и :

                                      ;

                                                   ;

                                .

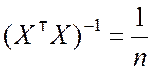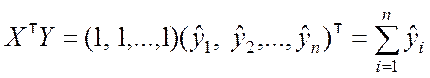Окончательно получим

                                        .

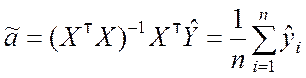Заметим, что решение совпадает с полученным в примере 8.1.

Эта оценка является несмещённой и эффективной. Определим точность оценки . На основании формулы (8.3.14) получим

                                                ,  

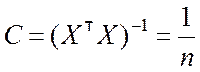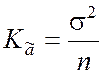                                                        .                      (8.3.17)

Если бы величина s² не была априори известной, то её оценку можно было бы получить на основании формулы (8.3.16):

                                                .                            

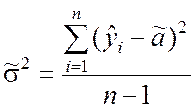Затем можно найти дисперсию оценки  по формуле (8.3.17) с заменой  s²  на  .

Данный пример фактически указывает, каким образом следует оценивать математическое ожидание случайной величины и каковы при этом точечные характеристики этих оценок. Напомним, что ранее тот же результат для оценки математического ожидания был получен с помощью предельных теорем.

                                                                                                                ▲

П р и м е р 8.3. Рассмотрим задачу, аналогичную приведённой в примере 8.2, с тем отличием, что независимые измерения величины a производятся с различной от эксперимента к эксперименту точностью, которая характеризуется дисперсией , .

▼ Итак, имеем схему неравноточных наблюдений:

    ;    ;    .

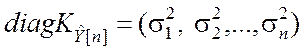Корреляционная матрица  взята в диагональной форму в силу независимости измерений.

Данную задачу сводим к предыдущей, используя преобразования (8.3.6), (8.3.7). При этом

                                                  ,

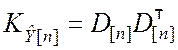где D – диагональная матрица с диагональю

                                         .

Тогда формула (8.3.7) приводит к новому вектору

                                       .

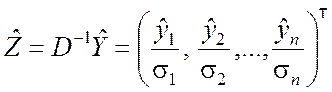Легко убедиться, что корреляционная матрица вектора  получается при этом единичной, а задача сводится к предыдущей. Уравнение (8.3.3) записывается в виде

                                                ,

где   .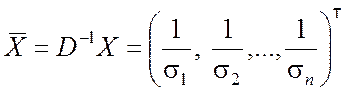

Далее находим, как и в примере 8.2:

       ;    ;     ;

                                    .

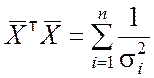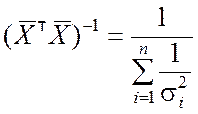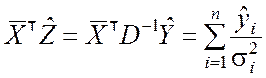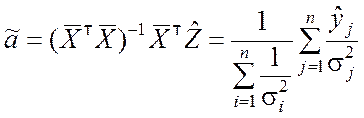Данная оценка является несмещённой и эффективной, причём

                                                     .

▲

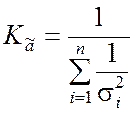Сравнивая полученное решение с решением задачи 8.1 или 8.2, видим, что учёт неравноточности измерений приводит к иному решению. Возвращаясь к замечанию, указанному в примере 8.1, можно опять же подчеркнуть, что учёт статистических свойств ошибок измерений приводит к необходимости иного выбора функции V(a), чем это было сделано в примере 8.1 или 8.2.