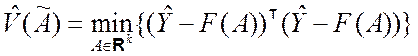Статистический анализ экспериментальных данных методом наименьших квадратов (Раздел 8 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 3

                                ,   (8.2.5)

где  – вектор, представляющий собой решение задачи (8.2.5);  R^k – k- мерное вещественное пространство.

Часто вместо минимизации квадратичной функции (8.2.5) для оценивания вектора A используют минимизацию квадратичной функции более общего вида:

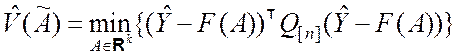                             , (8.2.6)

где Q_[n] – неотрицательно определённая симметричная матрица, которая называется весовой.

Очевидно, что задача (8.2.5) является частным случаем задачи (8.2.6), если в качестве весовой выбрать единичную матрицу.

Показатель качества оценивания (8.2.5) в скалярной форме имеет вид

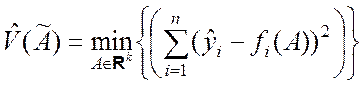                                    ,       (8.2.7)

где  и f_i,  – компоненты вектора Y и вектор-функции F соответственно.

Скалярная форма показателя (8.2.6):

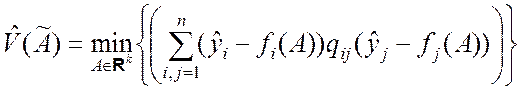                         ,                                                         (8.2.8)

Для сокращения записей, а также упрощения некоторых выкладок в последующем будем использовать в основном векторно-матричную запись показателя качества оценивания вектора A.

Необходимое условие минимума функции (8.2.5) или (8.2.6) состоит в том, что её частные производные по всем компонентам a_i вектора A должны быть равны нулю:

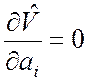                                                ,    .                   (8.2.9)

Развёрнутый вид условий (8.2.9) в скалярной форме представляется следующей системой уравнений:

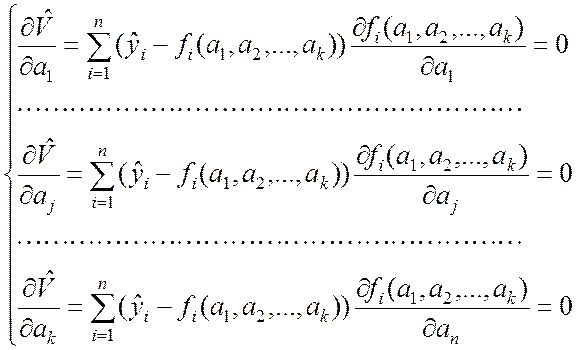                                                                              (8.2.10)

Система уравнений (8.2.10) в теории МНК называется системой нормальных уравнений. Её решение, т.е. вектор  будем в дальнейшем называть МНК-оценкой.

П р и м е р 8.1. Требуется оценить скалярную величину a, для которой уравнение наблюдения имеет вид

                                              ,   .

▼ Предположим, что оценку параметра a необходимо отыскивать минимизацией суммы квадратов отклонений

                                               .

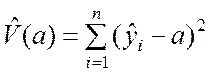Тогда необходимое условие минимума этой суммы квадратов в соответствии с (8.2.9) запишется в виде

                                  .

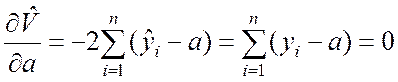Оценка искомой величины

                                                     .

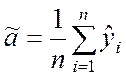Следует заметить, что при решении данной задачи обоснование выбора функции V(a) отсутствовало, хотя ранее в § 2.4 указывалось, что оптимальный выбор данной функции диктуется условиями задачи.

Замечание приведено в связи с тем, что в дальнейшем будет даваться и иное решение этой же задачи.                                                         ▲

В общем случае система нормальных уравнений нелинейная относительно искомых параметров, а искомые параметры – компоненты вектора A – выражаются нелинейным образом через компоненты вектора наблюдения .

8.3. Метод наименьших квадратов при линейной связи наблюдаемых и оцениваемых параметров

8.3.1. Линейная модель наблюдения

Рассматриваемый ниже метод наименьших квадратов при линейной модели наблюдения получил название схемы Гаусса–Маркова.

Пусть наблюдаемые параметры и параметры искомой функциональной зависимости связаны линейным уравнением, а ошибки наблюдения аддитивны, причём имеют равные нулю математические ожидания:

                                           ,              (8.3.1)

                                                    ,                      (8.3.2)

где X_[n;k] – прямоугольная матрица, называемая матрицей наблюдения;  и , как и ранее, соответственно случайные векторы наблюдения и ошибок наблюдения.

На основании равенства (8.3.2) можно записать

                                             .                (8.3.3)

В модели Гаусса–Маркова предполагается, что относительно вектора  известна некоторая дополнительная информация. Рассмотрим возможные варианты использования данной информации.