Статистический анализ экспериментальных данных методом наименьших квадратов (Раздел 8 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 5

                                               .                (8.3.12)

Если относительно вектора ошибок ничего не известно, то ничего нельзя сказать и о свойствах оценок (8.3.11) или (8.3.12). Если же соотношение (8.3.2) выполняется, то оценки (8.3.11), (8.3.12) являются несмещёнными. Действительно

поскольку  = 0.

Пусть корреляционная матрица вектора ошибок наблюдений имеет вид (8.3.4). Вычислим корреляционную матрицу вектора оценок . Обозначим

                                    ;   .

В этих обозначениях формула для МНК-оценки (8.3.11) перепишется в виде

                                               ,                           

где  .

Тогда корреляционная матрица вектора оценок  вычисляется по формуле

    

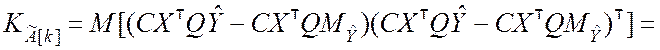
                                    (8.3.13)

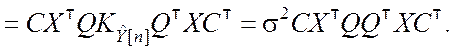
В процессе преобразований в выражении (8.3.13) учтено, что

                                 ,    .

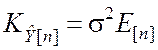Если Q = E, то

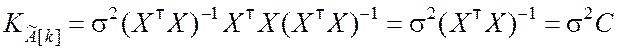                  .                                                        (8.3.14)

На практике наиболее часто используется вариант МНК-оценивания, при котором в качестве весовой матрицы Q выбирается матрица , поскольку в таком случае МНК-оценка получается эффективной. Доказательство этого факта можно найти, например, в [10]. Для такого варианта корреляционная матрица оценки вычисляется по формуле

                                               ,

которая  при  совпадает с выражением (8.3.14).

Когда величина s² известна, формулы (8.3.13), (8.3.14) позволяют отыскать корреляционную матрицу вектора . Из данных формул следует, что даже при некоррелированных равноточных наблюдениях компоненты вектора оценок оказываются коррелированными. Для их некоррелированности необходима ещё ортогональность столбцов матрицы наблюдений X (при Q = E) или столбцов матрицы в общем случае.

Если дисперсия наблюдений s² неизвестна, её необходимо оценить наряду с компонентами вектора A, иначе невозможно отыскать корреляционную матрицу вектора , которая даёт характеристики точности оценивания.

Покажем, каким образом можно получить оценку величины s². В математической статистике доказывается, что остаточная сумма квадратов

                                                   (8.3.15)

( – МНК-оценка при линейной модели наблюдения) имеет закон распределения , если вектор ошибок наблюдения  характеризуется корреляционной матрицей s²E (n – размерность вектора ,  k – число оцениваемых параметров).

В скалярной форме выражение (8.3.15) имеет вид

                                  .

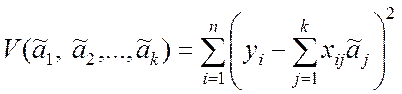На основании свойств  - распределения получается, что

                                             ,

а потому оценку для величины s² можно приближённо вычислять по формуле

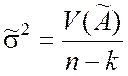                                                     .                      (8.3.16)

Отметим, что это оценка несмещённая.

Без доказательства укажем, что МНК-оценки не всегда получаются эффективными. Ранее уже отмечалось со ссылкой на работу [10], что свойством эффективности обладают МНК-оценки для моделей наблюдения (8.3.3),  (8.3.4)  при Q = E,  (8.3.3), (8.3.5) при Q = G^–1 и (8.3.3), (8.3.8)  при  Q = R^–1. Это следует, в частности, для нормального распределения вектора ошибок  из эффективности оценок, получаемых по методу максимального правдоподобия, поскольку МНК и ММП-оценки совпадают при указанном способе выбора весовых матриц. При всех остальных способах выбора матрицы весов МНК-оценки неэффективны. Однако это не означает, что варианты выбора матрицы весов Q, приводящие к неэффективным оценкам, нецелесообразны. Различные соображения могут привести к выбору матрицы весов в другой форме.

П р и м е р 8.2. Известно, что величина a – постоянная, схема оценивания имеет вид